Nur L

14 Oktober 2024 14:28
Iklan
Nur L

14 Oktober 2024 14:28
Pertanyaan
diketahui suku pertama pada suatu baris aritmatika adalah 5 dan suku ke sepuluh dua kali dari suku ke empat. tentukan jumlah 6 suku pertama
diketahui suku pertama pada suatu baris aritmatika adalah 5 dan suku ke sepuluh dua kali dari suku ke empat. tentukan jumlah 6 suku pertama
1
3
Iklan
Fredo D
19 Oktober 2024 09:21
<h1>55</h1><p>berikut jawaban yang bisa kamu lihat</p>
55
berikut jawaban yang bisa kamu lihat
· 5.0 (1)
Iklan
E. Nur
15 Oktober 2024 06:08
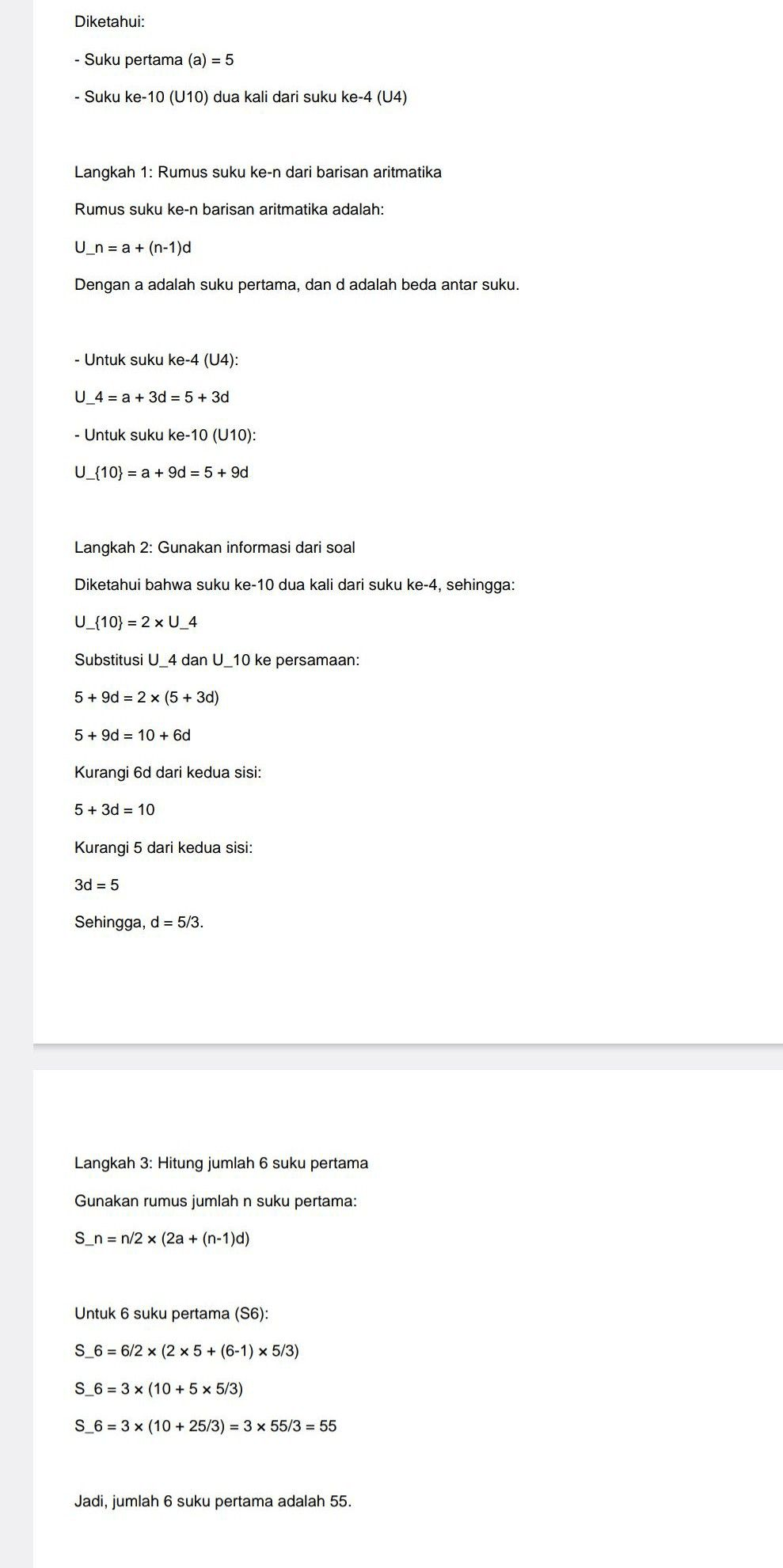
Jawaban: 55 Pembahasan pada gambar terlampir
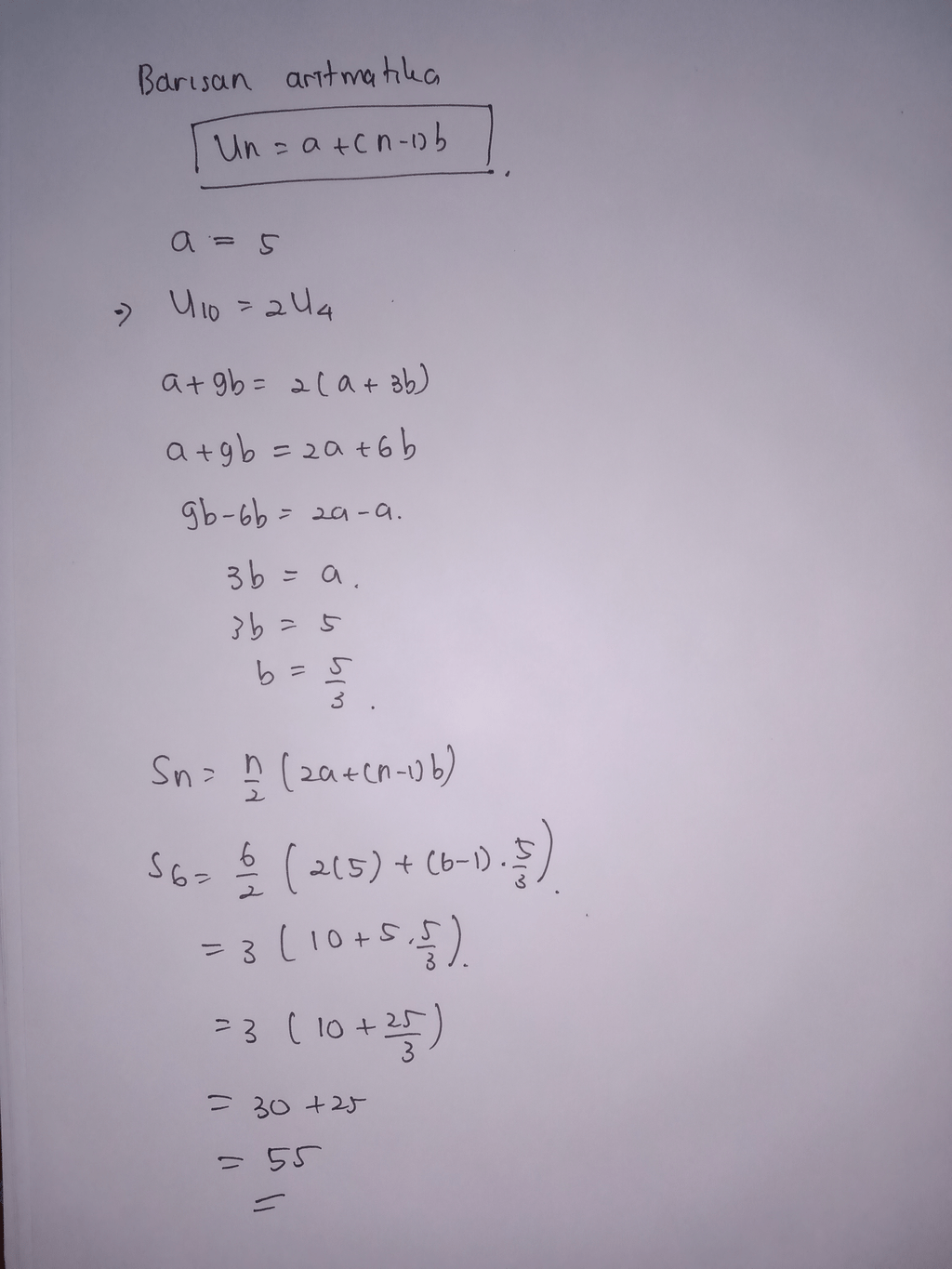
· 0.0 (0)
Iqbal I
16 Oktober 2024 03:06
<p>Diketahui:<br>- Suku pertama (U₁) = 5<br>- Suku ke-10 (U₁₀) dua kali dari suku ke-4 (U₄), yaitu U₁₀ = 2 × U₄</p><p>Rumus suku ke-n barisan aritmetika:<br>\[<br>U_n = U_1 + (n-1) \cdot b<br>\]<br>dengan \( b \) adalah beda barisan.</p><p>Langkah-langkah:<br>1. Suku ke-4:<br>\[<br>U_4 = U_1 + 3b = 5 + 3b<br>\]<br>2. Suku ke-10:<br>\[<br>U_{10} = U_1 + 9b = 5 + 9b<br>\]<br>3. Karena \( U_{10} = 2 \times U_4 \):<br>\[<br>5 + 9b = 2(5 + 3b)<br>\]<br>\[<br>5 + 9b = 10 + 6b<br>\]<br>\[<br>9b - 6b = 10 - 5<br>\]<br>\[<br>3b = 5<br>\]<br>\[<br>b = \frac{5}{3}<br>\]</p><p>4. Jumlah 6 suku pertama (S₆):<br>Rumus jumlah suku ke-n barisan aritmetika:<br>\[<br>S_n = \frac{n}{2} \cdot (U_1 + U_n)<br>\]<br>Untuk n = 6:<br>\[<br>S_6 = \frac{6}{2} \cdot (U_1 + U_6)<br>\]<br>Suku ke-6:<br>\[<br>U_6 = U_1 + 5b = 5 + 5 \times \frac{5}{3} = 5 + \frac{25}{3} = \frac{15}{3} + \frac{25}{3} = \frac{40}{3}<br>\]<br>Jadi:<br>\[<br>S_6 = 3 \cdot \left(5 + \frac{40}{3}\right) = 3 \cdot \frac{55}{3} = 55<br>\]</p><p>Jumlah 6 suku pertama adalah 55.</p>
Diketahui:
- Suku pertama (U₁) = 5
- Suku ke-10 (U₁₀) dua kali dari suku ke-4 (U₄), yaitu U₁₀ = 2 × U₄
Rumus suku ke-n barisan aritmetika:
\[
U_n = U_1 + (n-1) \cdot b
\]
dengan \( b \) adalah beda barisan.
Langkah-langkah:
1. Suku ke-4:
\[
U_4 = U_1 + 3b = 5 + 3b
\]
2. Suku ke-10:
\[
U_{10} = U_1 + 9b = 5 + 9b
\]
3. Karena \( U_{10} = 2 \times U_4 \):
\[
5 + 9b = 2(5 + 3b)
\]
\[
5 + 9b = 10 + 6b
\]
\[
9b - 6b = 10 - 5
\]
\[
3b = 5
\]
\[
b = \frac{5}{3}
\]
4. Jumlah 6 suku pertama (S₆):
Rumus jumlah suku ke-n barisan aritmetika:
\[
S_n = \frac{n}{2} \cdot (U_1 + U_n)
\]
Untuk n = 6:
\[
S_6 = \frac{6}{2} \cdot (U_1 + U_6)
\]
Suku ke-6:
\[
U_6 = U_1 + 5b = 5 + 5 \times \frac{5}{3} = 5 + \frac{25}{3} = \frac{15}{3} + \frac{25}{3} = \frac{40}{3}
\]
Jadi:
\[
S_6 = 3 \cdot \left(5 + \frac{40}{3}\right) = 3 \cdot \frac{55}{3} = 55
\]
Jumlah 6 suku pertama adalah 55.
· 0.0 (0)
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



