MR
Mila R
18 Maret 2022 12:52
Iklan
MR
Mila R
18 Maret 2022 12:52
Pertanyaan
diketahui sistem pertidaksamaan x+2y ≤14 , 3x+2y≤18 ,x≥0 dan y≥0 nilai maksimal dari fungsi obyektif f(x,y)= 2x+7y adalah...
2
1
Iklan
SR
S. Rofikoh
22 Maret 2022 05:10
Jawaban terverifikasi
Halo, Mila. Kakak bantu jawab, ya. Jawaban soal di atas adalah 49. Cermati pembahasan berikut ini. Diketahui sistem pertidaksamaan x+2y ≤14 , 3x+2y≤18 ,x≥0 dan y≥0. Ditanya nilai maksimal dari fungsi obyektif f(x,y)= 2x+7y. 1). Ubah pertidaksamaan menjadi persamaan untuk mendapat titik batasnya menjadi x+2y=14 dan 3x+2y=18. Untuk x=0 pada persamaan x+2y=14 x+2y=14 0+2y=14 2y=14 y=14/2 y=7 (x,y) = (0,7) Untuk y=0 pada persamaan x+2y=14 x+2y=14 x+2(0)=14 x+0=14 x=14 (x,y)=(14,0) Untuk x=0 pada persamaan 3x+2y=18 3x+2y=18 3(0)+2y=18 0+2y=18 2y=18 y=18/2 y=9 (x,y)=(0,9) Untuk y=0 pada persamaan 3x+2y=18 3x+2y=18 3x+2(0)=18 3x+0=18 3x=18 x=18/3 x=6 (x,y)=(6,0) 2). Uji titik (1,1) pada pertidaksamaan. (1,1) disubstitusikan ke pertidaksamaan x+2y ≤14 x+2y ≤14 1+2(1)≤14 1+2≤14 3≤14...benar Maka, arsir daerah yang memuat titik (1,1). (1,1) disubstitusikan ke pertidaksamaan 3x+2y≤18 3x+2y≤18 3(1)+2(1)≤18 3+2≤18 5≤18...benar Maka, arsir daerah yang memuat titik (1,1). Ingat! Untuk kendala non negatif x≥0 dan y≥0 maka arsir daerah pada kuadran I. Dengan demikian, daerah hasil penyelesaian digambarkan pada grafik di bawah ini dengan warna hijau. 3). Menghitung titik potong dengan menggunakan substitusi, pertidaksamaan diubah menjadi persamaan x+2y=14 dan 3x+2y=18. x+2y=14 (i) atau x=14-2y 3x+2y=18 (ii) x=14-2y disubstitusikan ke persamaan (ii) 3x+2y=18 3(14-2y)+2y=18 42-6y+2y=18 42-4y=18 -4y=18-42 -4y=-24 y=-24/-4 y=6 y=6 disubstitusikan ke persamaan (i) x+2y=14 x+2(6)=14 x+12=14 x=14-12 x=2 Diperoleh (x,y) = (2,6) 4. Menghitung nilai maksimal dari fungsi obyektif f(x,y)= 2x+7y Titik (6,0) f(x,y)= 2x+7y = 2(6) + 7(0) = 12+0 = 12 Titik (2,6) f(x,y)= 2x+7y = 2(2) + 7(6) = 4 + 42 = 46 Titik (0,7) f(x,y)= 2x+7y = 2(0)+7(7) = 0+49 = 49 (maksimal) Demikian, nilai maksimal berada pada titik (0,7) dengan nilai 49. Jadi, jawabannya adalah 49. Semoga membantu, ya.
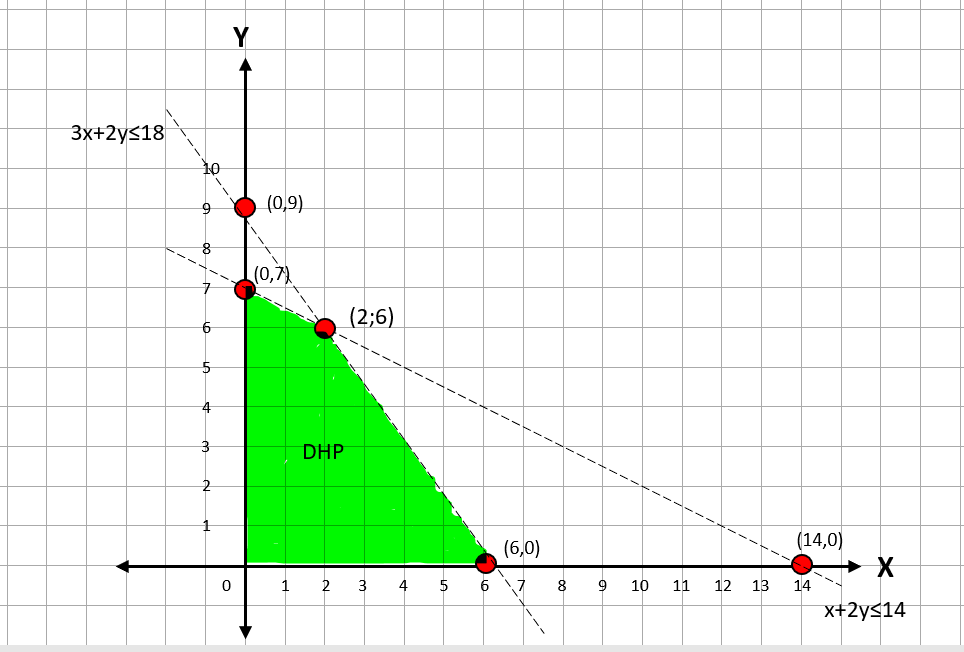
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



