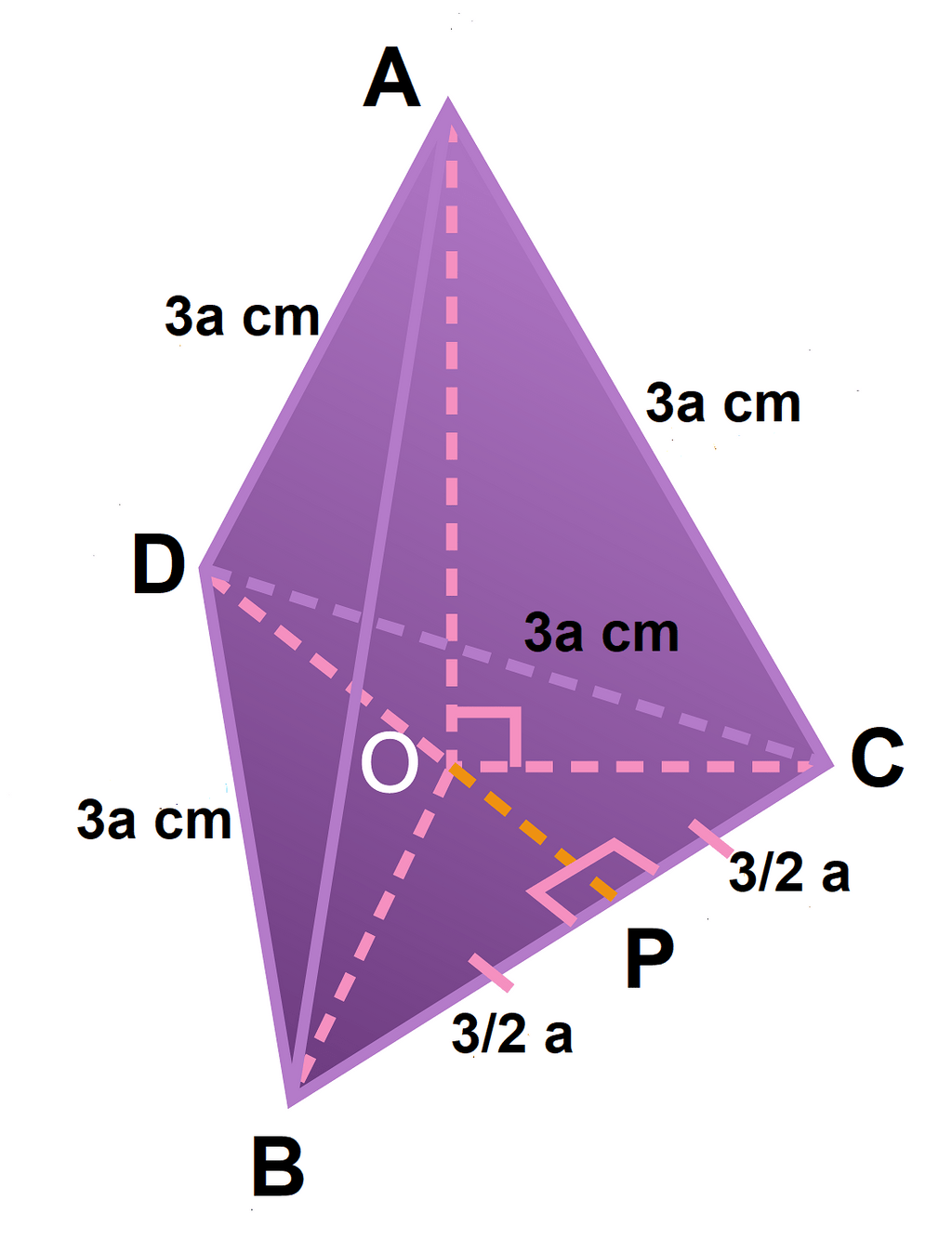
Diketahui limas DABC dengan alas berbentuk segitiga sama sisi. Panjang setiap rusuk limas tersebut adalah 3a cm. Jarak titik A ke bidang BCD adalah .... A. a√6 cm B. (a/3)√6 cm C. (a/2)√6 cm D. a√3 cm E. (a/3)√3 cm

<p>Jawaban: A</p><p>&nbsp;</p><p>Ingat bahwa!</p><p>Teorema phytagoras</p><p>c²=a²+b²</p><p>Dengan</p><p>a dan b adalah sisi-sisi yang saling tegak lurus</p><p>c adalah sisi miring</p><p>Setiap garis berat berpotongan pada titik berat dengan bagian-bagiannya memiliki perbandingan 2:1, bagian terpanjang adalah titik berat dengan titik sudut ke masing-masing.</p><p>Jarak titik ke bidang adalah panjang ruas garis yang ditarik dari suatu titik sampai memotong tegak lurus suatu bidang.</p><p>&nbsp;</p><p>Diketahui: Limas D.ABC &nbsp;dengan panjang sisi 3a cm.</p><p>Ditanya: Jarak titik A ke bidang BCD</p><p>Jawab:</p><p>Perhatikan gambar berikut!</p><p>DP²=DB²-BP²</p><p>DP²=(3a)²-(3/2 a)²</p><p>DP²=9a²- 9/4 a²</p><p>DP²=36/4 a²- 9/4 a²</p><p>DP²=27/4 a^2&nbsp;</p><p>DP =±√(27/4 a²)^&nbsp;</p><p>DP =± 3a√3/2 &nbsp;</p><p>Karena panjang sisi tidak mungkin negatif maka pilih DP =3a√3/2 &nbsp;</p><p>&nbsp;</p><p>Titik O merupakan titik berat, maka DO:OP = 2:1 sehingga</p><p>DO = 2/3 DP</p><p>DO = 2/3 × 3a√3/2&nbsp;</p><p>DO = a√3 cm</p><p>&nbsp;</p><p>Jarak titik A ke BCD adalah panjang AO yang dapat ditentukan dengan cara berikut.</p><p>AO²=DA²-DO²</p><p>AO²=(3a)²-(a√3)²</p><p>AO²=9a²- 3a²</p><p>AO²= 6a^2&nbsp;</p><p>AO=±√(6a²)</p><p>AO =±a√6</p><p>Karena jarak tidak mungkin negatif maka pilih AO = a√6 cm.</p><p>&nbsp;</p><p>Jadi, jawaban yang tepat adalah A.</p>