Rifqi A
20 Agustus 2023 15:20
Iklan
Rifqi A
20 Agustus 2023 15:20
Pertanyaan
Diketahui kubus ABCD.EFGH dengan panjang rusuk 8 cm. Titik M adalah titik tengah BC. Tentukan M ke EG.
Diketahui kubus ABCD.EFGH dengan panjang rusuk 8 cm. Titik M adalah titik tengah BC. Tentukan M ke EG.
1
2
Iklan
Ahmad A
20 Agustus 2023 17:09
<p>Dalam kubus ABCD.EFGH dengan panjang rusuk 8 cm, dan titik M adalah titik tengah BC, kita dapat mencari jarak dari titik M ke sisi EG.</p><p>Pertama-tama, perhatikan bahwa titik M adalah titik tengah dari sisi BC. Karena panjang rusuk kubus adalah 8 cm, maka panjang sisi BC adalah 8 cm. Oleh karena itu, panjang BM adalah setengah dari panjang BC:</p><p>BM = 8 cm / 2 = 4 cm</p><p>Selanjutnya, karena kubus adalah benda simetris, titik M dan titik E (yang merupakan titik tengah dari sisi FG yang berlawanan) terletak pada diagonal kubus yang sama. Dalam kasus ini, diagonal kubus adalah diagonal yang menghubungkan dua titik diagonal berlawanan, yaitu diagonal AC dan diagonal EH.</p><p>Panjang diagonal kubus bisa dihitung menggunakan teorema Pythagoras:</p>
Dalam kubus ABCD.EFGH dengan panjang rusuk 8 cm, dan titik M adalah titik tengah BC, kita dapat mencari jarak dari titik M ke sisi EG.
Pertama-tama, perhatikan bahwa titik M adalah titik tengah dari sisi BC. Karena panjang rusuk kubus adalah 8 cm, maka panjang sisi BC adalah 8 cm. Oleh karena itu, panjang BM adalah setengah dari panjang BC:
BM = 8 cm / 2 = 4 cm
Selanjutnya, karena kubus adalah benda simetris, titik M dan titik E (yang merupakan titik tengah dari sisi FG yang berlawanan) terletak pada diagonal kubus yang sama. Dalam kasus ini, diagonal kubus adalah diagonal yang menghubungkan dua titik diagonal berlawanan, yaitu diagonal AC dan diagonal EH.
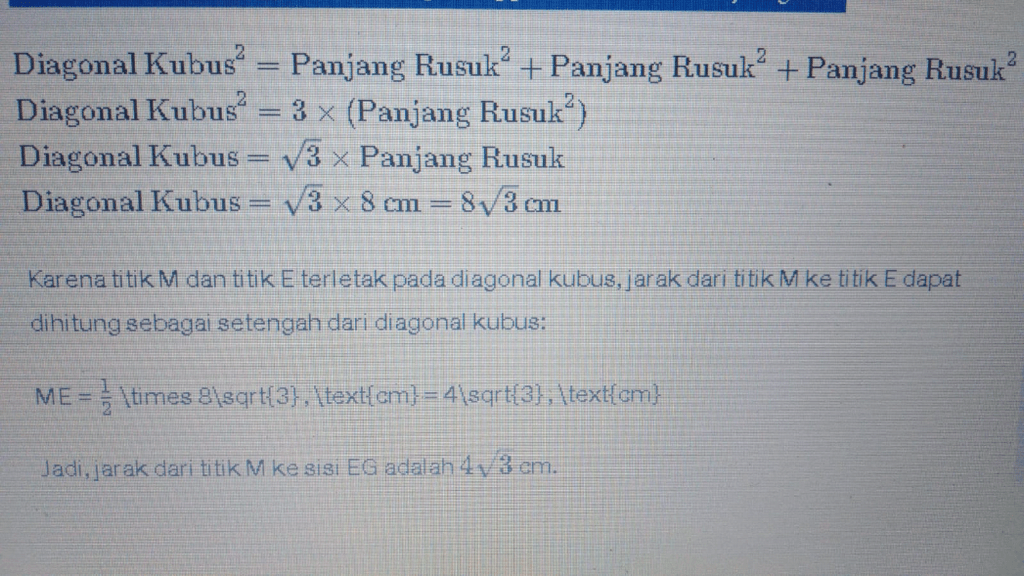
Panjang diagonal kubus bisa dihitung menggunakan teorema Pythagoras:
· 0.0 (0)
Iklan
Ab C
21 Agustus 2023 02:43
<p>Kubus</p><p>r = 8 cm</p><p> </p><p>M tengah BC</p><p> </p><p>Perhatikan ∆EMG</p><p>Dengan sisi :</p><p>EG = r√2 cm</p><p>EM = 3/2 cm</p><p>MG = 1/2 r√5 cm</p><p> </p><p>Dengan <strong>aturan cosinus </strong>diperoleh ∠GEC = 45°</p><p>X pada EG</p><p>MX ⊥ EG </p><p> </p><p><strong>Jarak M ke EG</strong></p><p>= MX</p><p>= EM cos ∠GEC</p><p>= 3/2 r × cos 45°</p><p>= 3/2 × 8 × 1/2 √2</p><p>= <strong>6√2 cm </strong></p>
Kubus
r = 8 cm
M tengah BC
Perhatikan ∆EMG
Dengan sisi :
EG = r√2 cm
EM = 3/2 cm
MG = 1/2 r√5 cm
Dengan aturan cosinus diperoleh ∠GEC = 45°
X pada EG
MX ⊥ EG
Jarak M ke EG
= MX
= EM cos ∠GEC
= 3/2 r × cos 45°
= 3/2 × 8 × 1/2 √2
= 6√2 cm
· 0.0 (0)
Mau jawaban yang terverifikasi?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



