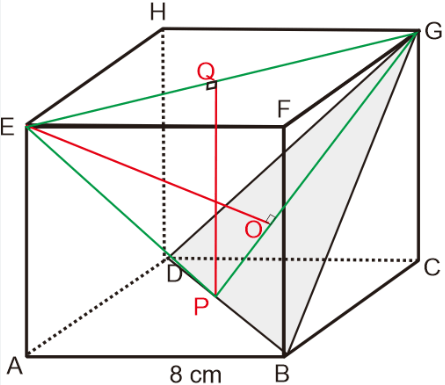
Diketahui kubus ABCD.EFGH dengan panjang rusuk 8 cm. Jarak titik E ke bidang BDG adalah... a. (1/3)√3 cm b. (2/3)√3 cm c. (4/3)√3 cm d. (8/3)√3 cm e. (16/3)√3 cm

Question

Jawaban yang benar adalah E. (16/3)√3 cm.

Diketahui:

Kubus ABCD.EFGH

Panjang rusuk = 8 cm

Ditanya:

Jarak titik E ke bidang BDG = ...?

Jawab:

Konsep yang kita gunakan adalah dimensi tiga. Pada sebuah bangun segitiga siku-siku berlaku teorema Pythagoras:

c² = a² + b².

Keterangan:

c = sisi miring (sisi terpanjang)

a dan b = sisi yang saling tegak lurus.

• Luas segitiga = 1/2 x alas x tinggi.

Perhatikan gambar pada foto di bawah. Garis EO adalah jarak bidang BDG dengan titik E.

1) Hitung panjang EG

Perhatikan segitiga EFG dengan siku-siku di F, diperoleh:

EG² = EF² + FG²

EG² = 8² + 8²

EG² = 64 + 64

EG = ±√(64 x 2)

EG = ±8√2 cm.

Panjang bernilai positif, maka EG = 8√2 cm.

2) Hitung panjang PG

Perhatikan segitiga PQG dengan siku-siku di Q, diperoleh:

PG² = PQ² + QG²

PG² = 8² + (4√2)² ---> QG = ½ × EG = ½ × 8√2 = 4√2 cm

PG² = 64 + 32

PG = ±√(96)

PG = ±√(16 x 6)

PG = ±4√6 cm.

Panjang bernilai positif, maka PG = 4√6 cm.

3) Dari segitiga EPG diperoleh:

Luas segitiga EPG = Luas segitiga EPG

1/2 x EG x PQ = 1/2 x PG x EO

EG x PQ = PG x EO

8√2 x 8 = 4√6 x EO

64√2 = 4√6 x EO

EO = (16√2/√6) x (√6/√6) ---> dirasionalkan

EO = 16√12 / (√6)²

EO = 16√(4x3) / 6

EO = 16x2√3/6

EO = 32√3/6 ---> bagikan dengan (2/2)

EO = (16/3)√3 cm.

Dengan demikian, jarak titik E ke bidang BDG adalah (16/3)√3 cm.

Oleh karena itu, jawaban yang benar adalah E.

Pertanyaan serupa