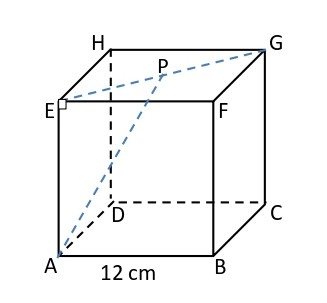
Diketahui kubus ABCD.EFGH dengan panjang rusuk 12 cm. Tentukan jarak: Titik A ke titik P, dimana P di tengah EG

Jawaban yang benar adalah 6√6 cm Ingat kembali: Dua titik dalam ruang yang berbeda posisi akan terletak pada satu garis. Jarak kedua titik tersebut sama dengan panjang garis yang menghubungkan kedua titik. Panjang diagonal bidang kubus = s√2 dimana: s = panjang sisi Pada segitiga siku-siku berlaku Teorema Phytagoras yaitu: c² = a² + b² dimana: c = panjang sisi miring a, b = panjang sisi-sisi penyiku Diketahui: Kubus ABCD.EFGH: s = 12 cm Ditanya: Jarak titik T ke titik G = ... Jawab: EG merupakan diagonal sisi maka panjang EG diperoleh: EG = s√2 EG = 12√2 cm P merupakan titik tengah EG sehingga: EP = ½ × 12√2 EP = 6√2 cm Jarak titik A ke titik P sama dengan panjang garis AP sehingga: AP² = EP² + AE² AP² = (6√2)² + 12² AP² = {6² × (√2)²} + 12² AP² = (36 × 2) + 144 AP² = 72 + 144 AP² = 216 AP = ±√216 AP = ±√(36 × 6) AP = ±√36 × √6 AP = ±√(6²) × √6 AP = ±6√6 Karena ukuran panjang selalu positif maka yang memenuhi adalah AP = 6√6 cm Jadi, jarak titik A ke titik P adalah 6√6 cm