Aulia R
31 Januari 2023 02:41
Iklan
Aulia R
31 Januari 2023 02:41
Pertanyaan
Diketahui balok ABCD. EFGH dengan panjang AB = 8 em, BC = 6 em, dan AE = 24 em. Titik X merupakan pertengahan rusuk DH. Jarak titik X ke garis AC adalah OX. a. Tentukan panjang AG!
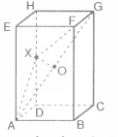
1
1
Iklan
Y. Frando
27 September 2023 02:19
<p>Jawaban yang benar adalah 26 cm.</p><p> </p><p>Pembahasan:</p><p>Ingat konsep berikut!</p><p>Pada suatu segitiga siku-siku berlaku teorema Pythagoras yaitu:</p><p>c<sup>2</sup> = a<sup>2</sup> + b<sup>2</sup>,</p><p> </p><p>dimana: a = sisi mendatar segitiga (cm), b = sisi tegak segitiga (cm), dan c = sisi miring segitiga (cm).</p><p> </p><p>Dari gambar soal di atas, terlihat bahwa garis AG adalah sisi miring segitiga siku-siku ACG. Maka, hitung panjang garis AC terlebih dahulu menggunakan teorema Pythagoras.</p><p>AC<sup>2</sup> = AB<sup>2</sup> + BC<sup>2</sup></p><p>AC<sup>2</sup> = 8<sup>2</sup> + 6<sup>2</sup></p><p>AC<sup>2</sup> = 64 + 36</p><p>AC = ±√100</p><p>AC = ±10 cm.</p><p>Nilai panjang sisi yang diambil adalah positif, maka panjang AC = 10 cm.</p><p> </p><p>Panjang garis CG = AE = 24 cm, sehingga panjang garis AG memenuhi teorema Pythagoras yaitu:</p><p>AG<sup>2</sup> = AC<sup>2</sup> + CG<sup>2</sup></p><p>AG<sup>2</sup> = 10<sup>2</sup> + 24<sup>2</sup></p><p>AG<sup>2</sup> = 100 + 576</p><p>AG = ±√676</p><p>AG = ±26 cm.</p><p>Nilai panjang sisi yang diambil adalah positif, maka panjang AG = 26 cm.</p><p> </p><p>Jadi, panjang AG adalah 26 cm.</p>
Jawaban yang benar adalah 26 cm.
Pembahasan:
Ingat konsep berikut!
Pada suatu segitiga siku-siku berlaku teorema Pythagoras yaitu:
c2 = a2 + b2,
dimana: a = sisi mendatar segitiga (cm), b = sisi tegak segitiga (cm), dan c = sisi miring segitiga (cm).
Dari gambar soal di atas, terlihat bahwa garis AG adalah sisi miring segitiga siku-siku ACG. Maka, hitung panjang garis AC terlebih dahulu menggunakan teorema Pythagoras.
AC2 = AB2 + BC2
AC2 = 82 + 62
AC2 = 64 + 36
AC = ±√100
AC = ±10 cm.
Nilai panjang sisi yang diambil adalah positif, maka panjang AC = 10 cm.
Panjang garis CG = AE = 24 cm, sehingga panjang garis AG memenuhi teorema Pythagoras yaitu:
AG2 = AC2 + CG2
AG2 = 102 + 242
AG2 = 100 + 576
AG = ±√676
AG = ±26 cm.
Nilai panjang sisi yang diambil adalah positif, maka panjang AG = 26 cm.
Jadi, panjang AG adalah 26 cm.
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



