Nur A

25 September 2023 03:48
Iklan
Nur A

25 September 2023 03:48
Pertanyaan
Diketahui balok ABCD.EFGH dengan panjang 10 cm, lebar 8 cm dan tinggi 6 cm. P pada perpanjangan BC sehingga BP=2BC Jarak titik E ke P adalah
Diketahui balok ABCD.EFGH dengan panjang 10 cm, lebar 8 cm dan tinggi 6 cm. P pada perpanjangan BC sehingga BP=2BC Jarak titik E ke P adalah

1
2
Iklan
Elizabeth L
25 September 2023 04:07
<p>Jawaban di foto</p>
Jawaban di foto
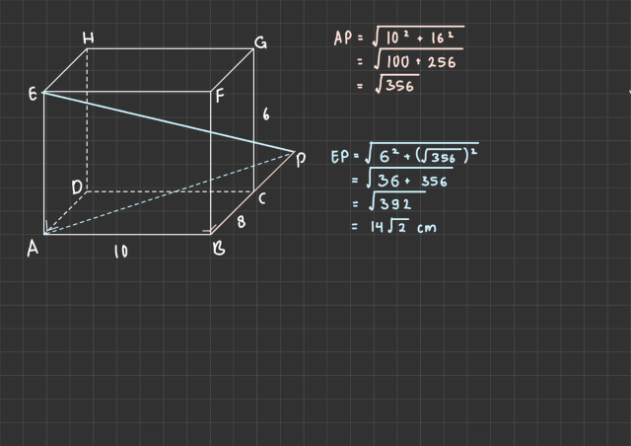
· 5.0 (1)
Iklan
H. Endah
Mahasiswa/Alumni Universitas Negeri Yogyakarta
25 September 2023 06:22
<p>Jawaban: 14√2 cm</p><p> </p><p>Konsep:</p><p>Rumus teorema phytagoras</p><p>c² = a² + b²</p><p>dengan a,b adalah sisi siku-siku dan c adalah sisi miring/hipotenusa</p><p> </p><p>Pembahasan:</p><p>Perhatikan gambar terlampir.</p><p>Diketahui balok ABCD.EFGH dengan:</p><p>panjang = AB = 10 cm</p><p>lebar = BC = 8 cm</p><p>tinggi = AE = 6 cm. </p><p>P pada perpanjangan BC sehingga BP = 2BC, maka:</p><p>BP = 2(8)</p><p>BP = 16 cm</p><p> </p><p>Pada ΔABP siku - siku di B didapatkan:</p><p>AP<sup>2</sup> = AB<sup>2</sup> + BP<sup>2</sup></p><p>AP<sup>2</sup> = 10<sup>2</sup> + 16<sup>2</sup></p><p>AP<sup>2</sup> = 100 + 256</p><p>AP<sup>2</sup> = 356</p><p> </p><p>Pada ΔEAP siku-siku di A didapatkan:</p><p>EP<sup>2</sup> = AE<sup>2</sup> + AP<sup>2</sup></p><p>EP<sup>2</sup> = 6<sup>2</sup> + 356</p><p>EP<sup>2</sup> = 36 + 356</p><p>EP<sup>2</sup> = 392</p><p>EP = ±√392</p><p>EP = ±14√2</p><p>Karena ukuran panjang tidak mungkin negatif, maka EP = 14√2 cm</p><p> </p><p>Jadi, jarak titik E ke P adalah 14√2 cm.</p>
Jawaban: 14√2 cm
Konsep:
Rumus teorema phytagoras
c² = a² + b²
dengan a,b adalah sisi siku-siku dan c adalah sisi miring/hipotenusa
Pembahasan:
Perhatikan gambar terlampir.
Diketahui balok ABCD.EFGH dengan:
panjang = AB = 10 cm
lebar = BC = 8 cm
tinggi = AE = 6 cm.
P pada perpanjangan BC sehingga BP = 2BC, maka:
BP = 2(8)
BP = 16 cm
Pada ΔABP siku - siku di B didapatkan:
AP2 = AB2 + BP2
AP2 = 102 + 162
AP2 = 100 + 256
AP2 = 356
Pada ΔEAP siku-siku di A didapatkan:
EP2 = AE2 + AP2
EP2 = 62 + 356
EP2 = 36 + 356
EP2 = 392
EP = ±√392
EP = ±14√2
Karena ukuran panjang tidak mungkin negatif, maka EP = 14√2 cm
Jadi, jarak titik E ke P adalah 14√2 cm.
· 5.0 (1)
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke Forum
Biar Robosquad lain yang jawab soal kamu

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



