Diberikan limas beraturan D.ABC yang panjang rusuknya 12 cm. Hitunglah Jarak titik D ke bidang ABC !

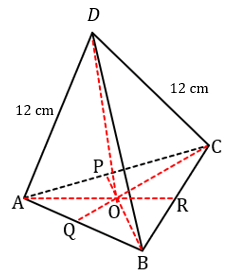
Jawaban yang benar adalah 4√6 cm. Diketahui: Limas beraturan D.ABC Panjang rusuk = 12 cm Ditanya: Jarak titik D ke bidang ABC = ...? Jawab: (i). Jarak titik ke bidang adalah lintasan terpendek yang menghubungkan titik dan tegak lurus terhadap bidang. (ii). Perbandingan garis tinggi segitiga adalah 2 : 1. (iv). Pada suatu segitiga siku-siku berlaku teorema Pythagoras yaitu: c^2 = a^2 + b^2, dimana: a = sisi mendatar segitiga (cm), b = sisi tegak segitiga (cm), dan c = sisi miring segitiga (cm). (i). Gambar limas D.ABC disajiikan seperti pada foto di bawah. Diperoleh bahwa AR, BP, dan CQ adalah garis berat segitiga ABC. Sehingga O adalah titik berat segitiga ABC. (ii). Selanjutnya cari proyeksi titik D ke bidang ABC. Karena D.ABC adalah bidang empat beraturan, maka proyeksi D ke bidang ABC akan terletak pada titik beratnya, yaitu titik O. Sehingga proyeksi titik D ke bidang ABC adalah titik O. Maka, jarak dari D ke bidang ABC sama dengan panjang ruas garis DO. (iii). Perhatikan juga bahwa AO : OR = 2 : 1. Karena bidang empat beraturan di atas memiliki panjang rusuk yang seluruhnya sama, maka segitiga ABC adalah segitiga sama sisi. Sehingga AR selain menjadi garis berat, juga menjadi garis tinggi. Maka segitiga ABR siku-siku di R. Karena AB = 12 cm dan BR = 6 cm, maka menggunakan Pythagoras didapat: AR^2 = AB^2 - BR^2 AR^2 = 12^2 - 6^2 AR^2 = 108 AR = 6√3 cm. Karena AO : OR = 2 : 1, maka didapatkan bahwa AO = 4√3 cm dan OR = 2√3 cm. (iv). Karena O adalah proyeksi D pada bidang ABC, maka DO tegak lurus dengan ABC, sehingga DO tegak lurus dengan seluruh garis pada bidang ABC, salah satunya AO. Jika diperhatikan segitiga ADO, siku-siku terletak di O, maka dari teorema Pythagoras diperoleh: DO^2 = AD^2 - AO^2 DO^2 = 12^2 - (4√3)^2 DO^2 = 144 - 48 DO = √96 DO = 4√6 cm. Jadi, jarak titik D ke bidang ABC adalah 4√6 cm.