Niko N
16 Februari 2023 01:05
Iklan
Niko N
16 Februari 2023 01:05
Pertanyaan
Diberikan kubus ABCD.EFGH dengan panjang rusuk 2p. Titik-titik P, Q, dan R masing-masing adalah titik tengah FB,FG, dan AD. Luas penampang irisan bidang yang melalui P, Q, dan R dan kubus ABCD.EFGH adalah ... A) 6p²√3 B) 3p²√3 C) p²√3 D) 3p²√2 E) 3p²/√6
2
1
Iklan
Y. Frando
02 Juli 2023 12:31
<p>Jawaban yang benar adalah B. 3p²√3.</p><p> </p><p>Diketahui:</p><p>Kubus ABCD.EFGH</p><p>Panjang rusuk = 2p.</p><p>Titik-titik P, Q, dan R masing-masing adalah titik tengah FB, FG, dan AD</p><p> </p><p>Ditanya:</p><p>Luas penampang irisan bidang yang melalui P, Q, dan R dan kubus ABCD.EFGH = ...?</p><p> </p><p>Jawab:</p><p>Untuk menghitung luas segitiga jika diketahui dua sisi dan salah satu sudut yang diapit oleh kedua sisi tersebut dapat menggunakan salah satu rumus berikut ini:</p><p>L = ½ x a x b x sin ∠C</p><p>L = ½ x a x c x sin ∠B</p><p>L = ½ x b x c x sin ∠A.</p><p> </p><p>Pada sebuah segitiga siku-siku berlaku teorema Pythagoras:</p><p>c² = a² + b².</p><p> </p><p>Keterangan:</p><p>c = sisi miring (sisi terpanjang)</p><p>a dan b = sisi yang saling tegak lurus.</p><p> </p><p>Gambar penampang irisan bidang yang melalui P, Q, dan R dan kubus ABCD.EFGH ditunjukkan pada foto di bawah. Terlihat bahwa dihasilkan gambar (1) berupa bangun segienam beraturan yaitu bidang JPQNMR.</p><p>Tinjau ΔJAR untuk menghitung panjang JR. Dari teorema Pythagoras diperoleh:</p><p>JR² = JA² + AR²</p><p>JR² = p² + p²</p><p>JR² = 2p²</p><p>JR = ±√(2p²)</p><p>JR = ±p√2.</p><p>Panjang sisi bernilai positif, maka JR = p√2.</p><p> </p><p>Selanjutnya tinjau ΔJOR pada gambar (2). Dikarenakan sudut dalam segitiga adalah sama, yaitu 360°/6 = 60° maka dihasilkan segitiga sama sisi, sehingga JR = JO = OR = p√2.</p><p>Kemudian hitung luas ΔJOR, sehingga diperoleh:</p><p>Luas ΔJOR = ½ x JO x OR x sin ∠O</p><p>Luas ΔJOR = ½ x p√2 x p√2 x sin 60°</p><p>Luas ΔJOR = p<sup>2</sup> x ½√3</p><p>Luas ΔJOR = ½p<sup>2</sup>√3.</p><p> </p><p>Sehingga, luas penampang irisan bidang yang melalui P, Q, dan R dan kubus ABCD.EFGH adalah:</p><p>L = 6 x Luas ΔJOR</p><p>L = 6 x ½p<sup>2</sup>√3</p><p>L = 3p<sup>2</sup>√3.</p><p> </p><p>Oleh karena itu, jawaban yang benar adalah B.</p>
Jawaban yang benar adalah B. 3p²√3.
Diketahui:
Kubus ABCD.EFGH
Panjang rusuk = 2p.
Titik-titik P, Q, dan R masing-masing adalah titik tengah FB, FG, dan AD
Ditanya:
Luas penampang irisan bidang yang melalui P, Q, dan R dan kubus ABCD.EFGH = ...?
Jawab:
Untuk menghitung luas segitiga jika diketahui dua sisi dan salah satu sudut yang diapit oleh kedua sisi tersebut dapat menggunakan salah satu rumus berikut ini:
L = ½ x a x b x sin ∠C
L = ½ x a x c x sin ∠B
L = ½ x b x c x sin ∠A.
Pada sebuah segitiga siku-siku berlaku teorema Pythagoras:
c² = a² + b².
Keterangan:
c = sisi miring (sisi terpanjang)
a dan b = sisi yang saling tegak lurus.
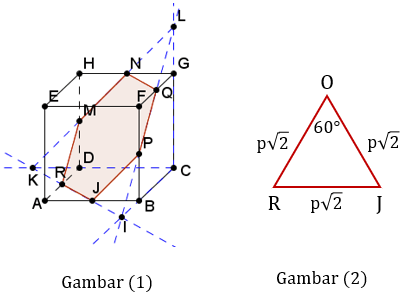
Gambar penampang irisan bidang yang melalui P, Q, dan R dan kubus ABCD.EFGH ditunjukkan pada foto di bawah. Terlihat bahwa dihasilkan gambar (1) berupa bangun segienam beraturan yaitu bidang JPQNMR.
Tinjau ΔJAR untuk menghitung panjang JR. Dari teorema Pythagoras diperoleh:
JR² = JA² + AR²
JR² = p² + p²
JR² = 2p²
JR = ±√(2p²)
JR = ±p√2.
Panjang sisi bernilai positif, maka JR = p√2.
Selanjutnya tinjau ΔJOR pada gambar (2). Dikarenakan sudut dalam segitiga adalah sama, yaitu 360°/6 = 60° maka dihasilkan segitiga sama sisi, sehingga JR = JO = OR = p√2.
Kemudian hitung luas ΔJOR, sehingga diperoleh:
Luas ΔJOR = ½ x JO x OR x sin ∠O
Luas ΔJOR = ½ x p√2 x p√2 x sin 60°
Luas ΔJOR = p2 x ½√3
Luas ΔJOR = ½p2√3.
Sehingga, luas penampang irisan bidang yang melalui P, Q, dan R dan kubus ABCD.EFGH adalah:
L = 6 x Luas ΔJOR
L = 6 x ½p2√3
L = 3p2√3.
Oleh karena itu, jawaban yang benar adalah B.
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



