Skuzyy S

15 Mei 2024 04:26
Iklan
Skuzyy S

15 Mei 2024 04:26
Pertanyaan
derajat polinomial P(x) hasil dan sisa dari : P(x) = x 4 -4x³+3x²-7x+2 dibagi dengan x²-3x+1. gunakan metode horner dan pembagian bersusun
derajat polinomial P(x) hasil dan sisa dari :
P(x) = x4-4x³+3x²-7x+2 dibagi dengan x²-3x+1. gunakan metode horner dan pembagian bersusun
6
2
Iklan
E. Nur
15 Mei 2024 09:03
Pembahasan pada gambar terlampir
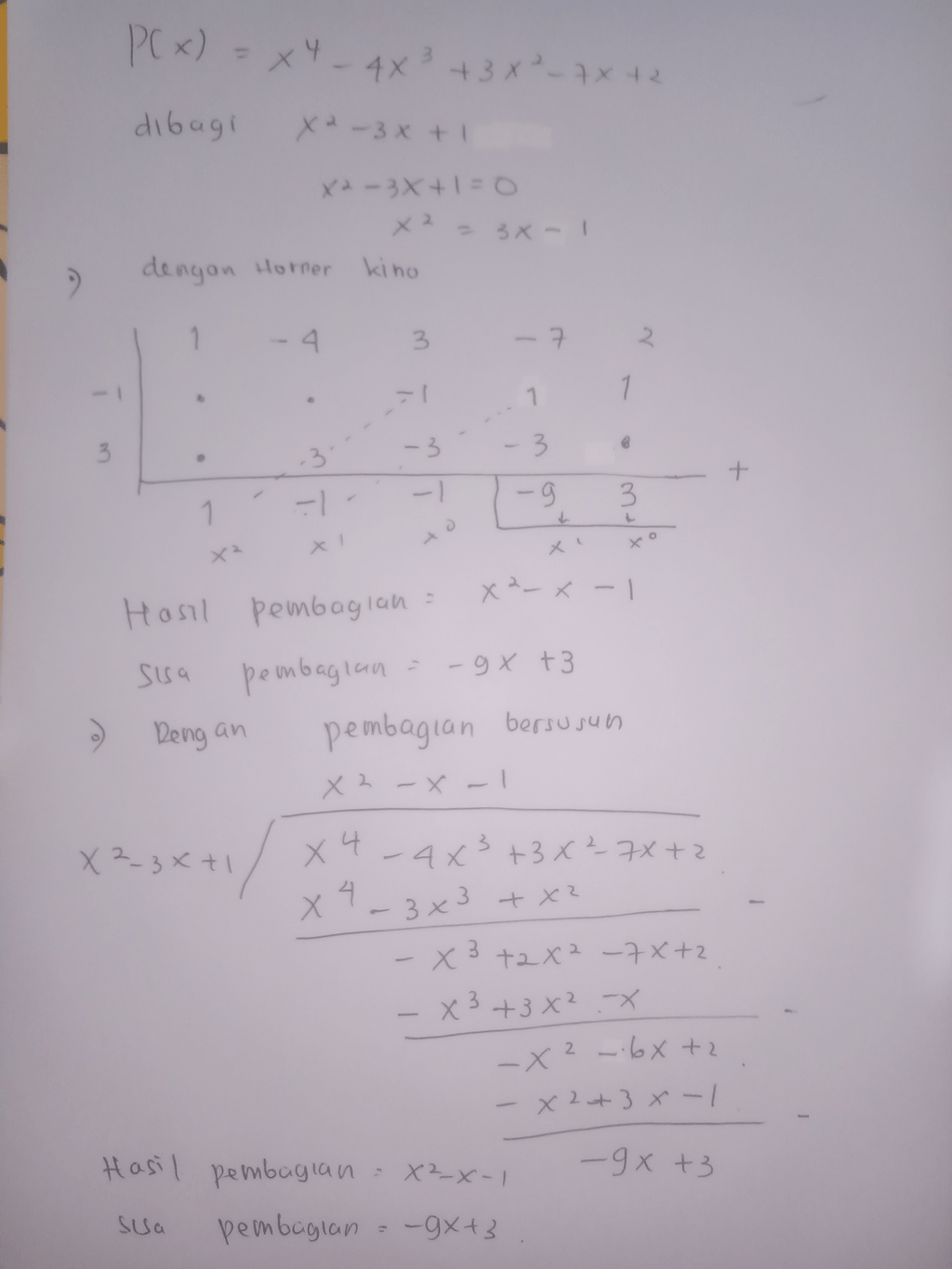
· 5.0 (1)
Iklan
Jacky J

Bronze
15 Mei 2024 07:25
<p><strong>Metode Horner</strong>: Pertama, kita perlu mengidentifikasi koefisien-koefisien dari (P(x)) dan pembagi (x^2 - 3x + 1):</p><ul><li>(a_0 = 2)</li><li>(a_1 = -7)</li><li>(a_2 = 3)</li><li>(a_3 = -4)</li><li>(a_4 = 1)</li></ul><p>Bagi (a_4 = 1) dengan (x^2 - 3x + 1):</p><ul><li>Hasil bagi: (x^2)</li><li>Sisa: (x^3 - 7x^2 + 3x - 5)</li></ul><p>Bagi (a_3 = -4) dengan (x^2 - 3x + 1):</p><ul><li>Hasil bagi: (-4x)</li><li>Sisa: (3x^2 - 5x + 3)</li></ul><p>Bagi (a_2 = 3) dengan (x^2 - 3x + 1):</p><ul><li>Hasil bagi: (3x + 6)</li><li>Sisa: (-11x + 9)</li></ul><p>Bagi (a_1 = -7) dengan (x^2 - 3x + 1):</p><ul><li>Hasil bagi: (-7)</li><li>Sisa: (-4x + 16)</li></ul><p>Bagi (a_0 = 2) dengan (x^2 - 3x + 1):</p><ul><li>Hasil bagi: (2)</li><li>Sisa: (10)</li></ul><p><strong>Pembagian Bersusun</strong>: Kita dapat menghitung hasil bagi dengan mengurutkan koefisien-koefisien dan mengurangkan setiap kali kita membagi:</p><p>[P(x) = (x^2 - 3x + 1)(x^2 - 4x + 3) + 10]</p><p>Jadi, hasil bagi adalah (x^2 - 4x + 3) dan sisa adalah (10).</p>
Metode Horner: Pertama, kita perlu mengidentifikasi koefisien-koefisien dari (P(x)) dan pembagi (x^2 - 3x + 1):
- (a_0 = 2)
- (a_1 = -7)
- (a_2 = 3)
- (a_3 = -4)
- (a_4 = 1)
Bagi (a_4 = 1) dengan (x^2 - 3x + 1):
- Hasil bagi: (x^2)
- Sisa: (x^3 - 7x^2 + 3x - 5)
Bagi (a_3 = -4) dengan (x^2 - 3x + 1):
- Hasil bagi: (-4x)
- Sisa: (3x^2 - 5x + 3)
Bagi (a_2 = 3) dengan (x^2 - 3x + 1):
- Hasil bagi: (3x + 6)
- Sisa: (-11x + 9)
Bagi (a_1 = -7) dengan (x^2 - 3x + 1):
- Hasil bagi: (-7)
- Sisa: (-4x + 16)
Bagi (a_0 = 2) dengan (x^2 - 3x + 1):
- Hasil bagi: (2)
- Sisa: (10)
Pembagian Bersusun: Kita dapat menghitung hasil bagi dengan mengurutkan koefisien-koefisien dan mengurangkan setiap kali kita membagi:
[P(x) = (x^2 - 3x + 1)(x^2 - 4x + 3) + 10]
Jadi, hasil bagi adalah (x^2 - 4x + 3) dan sisa adalah (10).
· 5.0 (2)
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



