Khumaira R
30 Januari 2023 07:55
Iklan
Khumaira R
30 Januari 2023 07:55
Pertanyaan
dengan menguraikan bentuk (b̅ - c̅) · (b̅ - c̅), Tunjukkan bahwa Ib̅I² + Ic̅I² - (b̅ - c̅)·(b̅ - c̅) = 2b̅ · c̅ ... *. Jika b̅=A̅C̅ dan c̅ = A̅B̅, simpulkan bahwa bentuk (∗) adalah aturan kosinus suatu segitiga ABC.
1
1
Iklan
Y. Frando
23 September 2023 07:52
<p>Jawaban yang benar adalah terbukti bahwa Ib̅I² + Ic̅I² - (b̅ - c̅)·(b̅ - c̅) = 2b̅ · c̅ dan bentuk (*) merupakan aturan kosinus suatu segitiga ABC.</p><p> </p><p>Pembahasan:</p><p>Ingat konsep berikut!</p><p>(i) b̅ · b̅ = Ib̅I²</p><p>(ii) b̅ · c̅ = Ib̅I . Ic̅I . cos θ</p><p>(iii) b̅ · c̅ = c̅ · b̅</p><p>(iv) Aturan cosinus pada segitiga ABC dengan panjang sisi AB = c, AC = b, dan BC = a yaitu:</p><p>a<sup>2</sup> = b<sup>2</sup> + c<sup>2</sup> - 2bc cos ∠A</p><p>b<sup>2</sup> = a<sup>2</sup> + c<sup>2</sup> - 2ac cos ∠B</p><p>c<sup>2</sup> = a<sup>2</sup> + b<sup>2</sup> - 2ab cos ∠C.</p><p> </p><p>Dari informasi soal, uraikan bentuk (b̅ - c̅) · (b̅ - c̅) untuk menunjukkan bentuk (*).</p><p> </p><p>Ib̅I² + Ic̅I² - (b̅ - c̅)·(b̅ - c̅) = 2b̅ · c̅</p><p>Ib̅I² + Ic̅I² - [b̅·b̅ - b̅·c̅ - b̅·c̅ + c̅·c̅] = 2b̅ · c̅</p><p>Ib̅I² + Ic̅I² - [Ib̅I² - 2b̅·c̅ + Ic̅I²] = 2b̅ · c̅</p><p>Ib̅I² + Ic̅I² - Ib̅I² + 2b̅·c̅ - Ic̅I² = 2b̅ · c̅</p><p>Ib̅I² - Ib̅I² + Ic̅I² - Ic̅I² + 2b̅·c̅ = 2b̅ · c̅</p><p>0 + 0 + 2b̅·c̅ = 2b̅ · c̅</p><p>2b̅ · c̅ = 2b̅ · c̅.</p><p>Terbukti bahwa bentuk (*) adalah benar dimana dengan menguraikan bentuk (b̅ - c̅) · (b̅ - c̅), diperoleh persamaan Ib̅I² + Ic̅I² - (b̅ - c̅)·(b̅ - c̅) = 2b̅ · c̅.</p><p> </p><p>Selanjutnya perhatikan segitiga ABC pada foto di bawah. Dari gambar tersebut diperoleh aturan cosinus yaitu:</p><p>BC<sup>2</sup> = AC<sup>2</sup> + AB<sup>2</sup> - 2.AC.AB.cos ∠A</p><p> </p><p>Dari penjumlahan vektor diperoleh:</p><p>AB + BC = AC</p><p>c̅ + BC = b̅</p><p>BC = b̅ - c̅.</p><p> </p><p>Maka, dari rumus aturan cosinus di atas diperoleh:</p><p>(b̅ - c̅)<sup>2</sup> = Ib̅I² + Ic̅I² - 2.Ib̅I.Ic̅I.cos θ</p><p>(b̅ - c̅) · (b̅ - c̅) = Ib̅I² + Ic̅I² - 2b̅ · c̅ ....(i)</p><p> </p><p>Dari bentuk penguraian (b̅ - c̅) · (b̅ - c̅) di atas sebelumnya telah diperoleh:</p><p>(b̅ - c̅) · (b̅ - c̅) = Ib̅I² + Ic̅I² - 2b̅ · c̅ ....(ii)</p><p> </p><p>Maka dapat disimpulkan bahwa bentuk (*) adalah aturan kosinus suatu segitiga ABC, karena persamaan bentuk (i) = (ii).</p><p> </p><p>Jadi, terbukti bahwa Ib̅I² + Ic̅I² - (b̅ - c̅)·(b̅ - c̅) = 2b̅ · c̅ dan bentuk (*) merupakan aturan kosinus suatu segitiga ABC.</p>
Jawaban yang benar adalah terbukti bahwa Ib̅I² + Ic̅I² - (b̅ - c̅)·(b̅ - c̅) = 2b̅ · c̅ dan bentuk (*) merupakan aturan kosinus suatu segitiga ABC.
Pembahasan:
Ingat konsep berikut!
(i) b̅ · b̅ = Ib̅I²
(ii) b̅ · c̅ = Ib̅I . Ic̅I . cos θ
(iii) b̅ · c̅ = c̅ · b̅
(iv) Aturan cosinus pada segitiga ABC dengan panjang sisi AB = c, AC = b, dan BC = a yaitu:
a2 = b2 + c2 - 2bc cos ∠A
b2 = a2 + c2 - 2ac cos ∠B
c2 = a2 + b2 - 2ab cos ∠C.
Dari informasi soal, uraikan bentuk (b̅ - c̅) · (b̅ - c̅) untuk menunjukkan bentuk (*).
Ib̅I² + Ic̅I² - (b̅ - c̅)·(b̅ - c̅) = 2b̅ · c̅
Ib̅I² + Ic̅I² - [b̅·b̅ - b̅·c̅ - b̅·c̅ + c̅·c̅] = 2b̅ · c̅
Ib̅I² + Ic̅I² - [Ib̅I² - 2b̅·c̅ + Ic̅I²] = 2b̅ · c̅
Ib̅I² + Ic̅I² - Ib̅I² + 2b̅·c̅ - Ic̅I² = 2b̅ · c̅
Ib̅I² - Ib̅I² + Ic̅I² - Ic̅I² + 2b̅·c̅ = 2b̅ · c̅
0 + 0 + 2b̅·c̅ = 2b̅ · c̅
2b̅ · c̅ = 2b̅ · c̅.
Terbukti bahwa bentuk (*) adalah benar dimana dengan menguraikan bentuk (b̅ - c̅) · (b̅ - c̅), diperoleh persamaan Ib̅I² + Ic̅I² - (b̅ - c̅)·(b̅ - c̅) = 2b̅ · c̅.
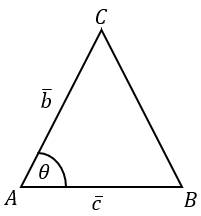
Selanjutnya perhatikan segitiga ABC pada foto di bawah. Dari gambar tersebut diperoleh aturan cosinus yaitu:
BC2 = AC2 + AB2 - 2.AC.AB.cos ∠A
Dari penjumlahan vektor diperoleh:
AB + BC = AC
c̅ + BC = b̅
BC = b̅ - c̅.
Maka, dari rumus aturan cosinus di atas diperoleh:
(b̅ - c̅)2 = Ib̅I² + Ic̅I² - 2.Ib̅I.Ic̅I.cos θ
(b̅ - c̅) · (b̅ - c̅) = Ib̅I² + Ic̅I² - 2b̅ · c̅ ....(i)
Dari bentuk penguraian (b̅ - c̅) · (b̅ - c̅) di atas sebelumnya telah diperoleh:
(b̅ - c̅) · (b̅ - c̅) = Ib̅I² + Ic̅I² - 2b̅ · c̅ ....(ii)
Maka dapat disimpulkan bahwa bentuk (*) adalah aturan kosinus suatu segitiga ABC, karena persamaan bentuk (i) = (ii).
Jadi, terbukti bahwa Ib̅I² + Ic̅I² - (b̅ - c̅)·(b̅ - c̅) = 2b̅ · c̅ dan bentuk (*) merupakan aturan kosinus suatu segitiga ABC.
· 5.0 (1)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



