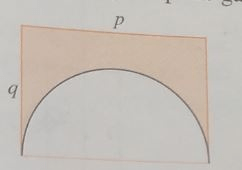
Dalam sebuah persegi panjang dibuat setengah lingkaran seperti pada gambar. Keliling daerah diarsir adalah 100. luas daerah diarsir akan maksimum untuk p =… a. 300/(4+3π) b. 200/(4+3π) c. 100/(4+3π) d. 200/(2+π) e. 100/(2+π)

<p>Jawaban : p = 50/(1+π)</p><p>&nbsp;</p><p>Ingat!&nbsp;</p><p>r = d/2</p><p>Keliling lingkaran = 2 · π · r&nbsp;</p><p>Luas lingkaran = &nbsp;π · r &nbsp;· r&nbsp;</p><p>dengan π = 22/7 atau 3,14&nbsp;</p><p>r : jari-jari&nbsp;</p><p>d : diameter</p><p>Luas persegi panjang = panjang x lebar</p><p>Jika diberikan persamaan y = ax² + bx + c, dengan a &lt; 0, maka nilai maksimumnya adalah D/(-4a)) dengan D = b²-4ac d0an nilai maksimum akan tecapai ketika -b/(2a)</p><p>&nbsp;</p><p>Diketahui lingkaran dengan</p><p>r = p/2</p><p>Persegi panjang dengan</p><p>panjang = p</p><p>lebar = q</p><p>Keliling daerah diarsir = 100</p><p>&nbsp;</p><p>Keliling daerah diarsir = 100</p><p>q+p+q+1/2 · 2 · π · r &nbsp;= 100</p><p>2q+p+π · r &nbsp;= 100</p><p>2q+p+π · p/2 &nbsp;= 100</p><p>2q+p+ pπ/2 &nbsp;= 100</p><p>2q = 100-p-pπ/2</p><p>q = 50-p/2-pπ/4</p><p>&nbsp;</p><p>Luas lingkaran = &nbsp;π · r &nbsp;· r&nbsp;</p><p>Luas lingkaran = π · p/2 · p/2</p><p>Luas lingkaran = p²π/4</p><p>&nbsp;</p><p>Luas persegi panjang = panjang x lebar</p><p>Luas persegi panjang = p x q</p><p>Luas persegi panjang = pq</p><p>&nbsp;</p><p>Luas yang diarsir = pq - p²π/4</p><p>Luas yang diarsir = p(50-p/2-pπ/4) - p²π/4</p><p>Luas yang diarsir = 50p - p²/2 - p²π/4 - p²π/4</p><p>Luas yang diarsir = 50p - p²/2 - p²π/2</p><p>Luas yang diarsir = - p²/2 - p²π/2 + 50p&nbsp;</p><p>Luas yang diarsir = -(1+π)/2 p² + 50p&nbsp;</p><p>&nbsp;</p><p>Diperoleh</p><p>a = -(1+π)/2</p><p>b = 50</p><p>c = 0</p><p>&nbsp;</p><p>Sehingga</p><p>-b/(2a)</p><p>= -50/(2.-(1+π)/2)</p><p>= -50/(-(1+π))</p><p>= 50/(1+π)</p><p>&nbsp;</p><p>Jadi, luas daerah diarsir akan maksimum untuk p = 50/(1+π)</p><p>Tidak ada pilihan jawaban yang benar</p>