MN
Moeh N
16 Desember 2021 03:19
Iklan
MN
Moeh N
16 Desember 2021 03:19
Pertanyaan
Daerah A berada pada kuadran pertama dan dibatasi oleh kurva y=x^(2) dan y=16. Daerah B dibatasi oleh kurva y=x^(2) dan garis y=4x, pernyataan berikut yang bernilai benar adalah ... A. Luas daerah A sama dengan luas daerah B. B. Luas daerah A : Luas daerah B=1:2. C. Luas daerah A : Luas daerah B=2:1. D. Luas daerah A : Luas daerah B=3:2. E. Luas daerah A : Luas daerah B=4:1.
2
2
Iklan
OA
O. Andrianto
04 Januari 2022 08:15
Jawaban terverifikasi
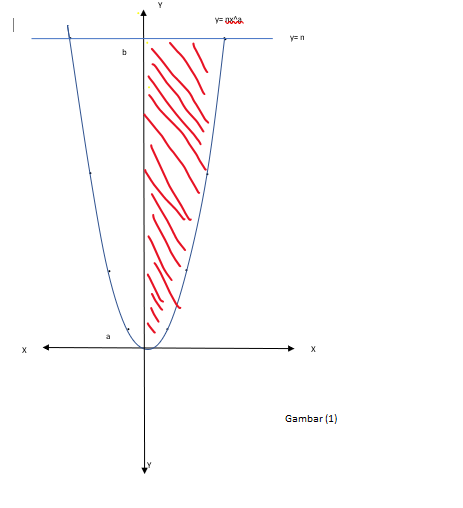
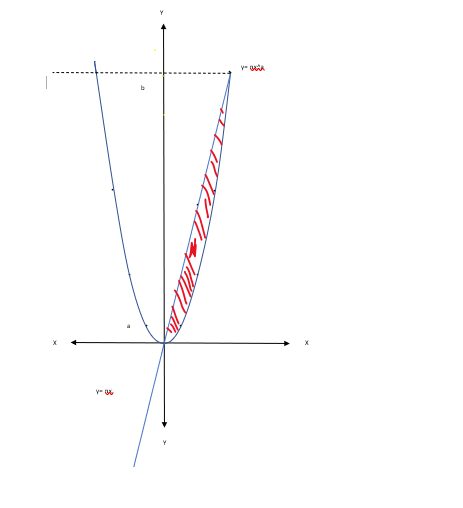
Halo Moeh N, Pernyataan yang benar adalah E. Luas daerah A : Luas Daerah B = 4 : 1 pada luas daerah A , terdapat 1 kurva, dan sumbu - y, yaitu y=nx^a dan y=n untuk mendapatkan luas daerah terebut, maka diperoleh rumus: L = ∫ f(y) dy , dengan batasan b dan a. Lihat gambar ke (1) pada luas daerah B, terdapat 2 kurva, yaitu yaitu y=nx^a dan y=nx untuk mendapatkan luas daerah terebut, maka diperoleh rumus: L = ∫ { f(y - g(y)} dy , dengan batasan b dan a. Lihat gambar ke (2)
· 0.0 (0)
Iklan
OA
O. Andrianto
04 Januari 2022 08:20
Jawaban terverifikasi
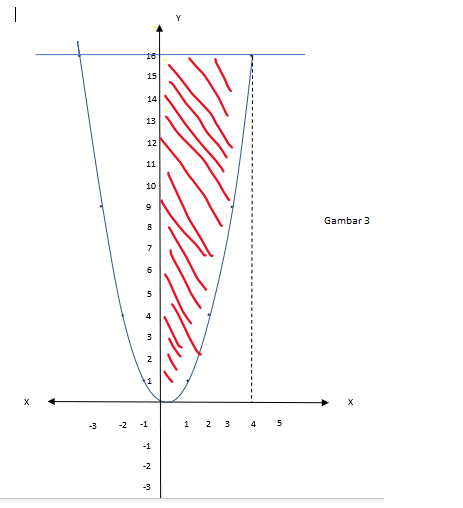
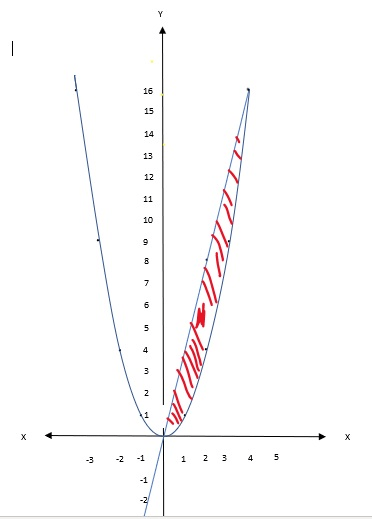
a. karena pada luas daerah A, dengan kurva y = x^2 , dan y=16, maka kita tentukan 1. kita membuat kurva seperti gambar ke 2, y1 = x^2 jika x =1 , maka y1 = (1) ^ 2 = 1 jika x =2, maka y1 = (2) ^ 2 = 4 jika x =3, maka y1 = (3)^2 = 9 jika x = 4, maka y1 = (4)^2 = 16 y2 = 16 3. karena pada soal menyebutkan kuadran pertama, maka bisa diliat pada gambar ke 3 terletak diantara b= 16 dan a = 0 , maka batasannya 16 dan 0 karena pada persamaan (1) y= x^2, maka kita ubah menjadi persamaan x, yaitu : x = √y L = ∫ f(y) dy , batasan b dan a L = ∫ √y dy, dengan batasnya 16 dan 0 L = |2/3 y^3/2|, batasnya 16 dan 0 L = {(2/3 x (16^3/2)) - (2/3 x (0^3/2))} L = (2/3 x (2^(2 x 3/2)) - 0 L = (2/3 x (8)) - 0 L = (128/3)- 0 = 128/3 b. karena pada luas daerah A, dengan kurva y = x^2 , dan y=4x, maka kita tentukan 1. persamaan y =x^2, maka kita ubah persamaan x, yaitu: x = √y 2. persamaan y = 4x, maka kita ubah persamaan x, yaitu: x=1/4 y L = ∫ f(y) - g(y) dy , batasan b dan a L = ∫ √y - 1/4 y dy, dengan batasnya 16 dan 0 L = |(2/3 y^3/2) - (1/8 y^2)|, batasnya 16 dan 0 L = {(2/3 x (16^3/2)) - (2/3 x (0^3/2))} - {(1/8 (16^2))- (1/8 (0^2))} L = {(2/3 x (2^(2 x 3/2)) - 0} - { (1/8 x 256) - 0} L = 128/3 - 32 L = 128/3 - 96/3 = 32 /3 maka perbandingan Luas daerah A ; Luas daerah B = 128/3 : 32/3 = 4:1 terima kasih sudah bertanya, semoga membantu ya
· 0.0 (0)
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke Forum
Biar Robosquad lain yang jawab soal kamu

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



