Sasa S
19 Januari 2024 06:17
Iklan
Sasa S
19 Januari 2024 06:17
Pertanyaan
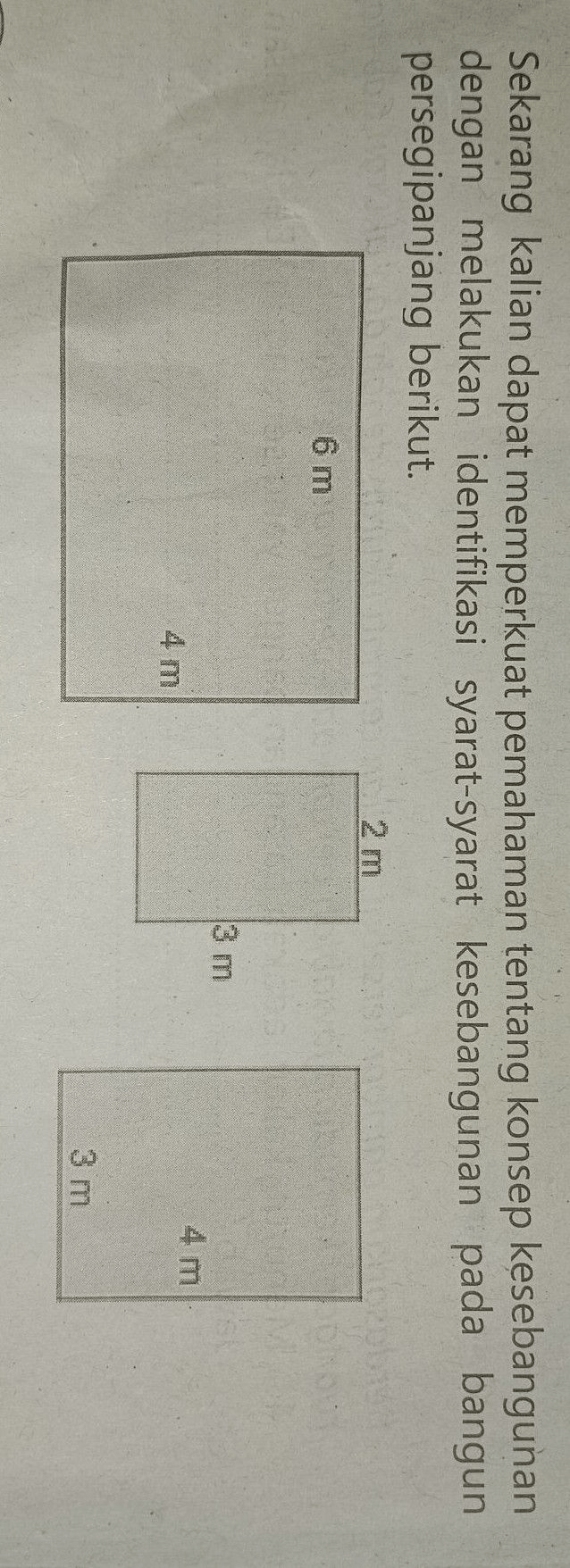
Berdasarkan gambar tersebut, jawablah pertanyaan berikut ini: 1. Apakah persegi panjang pertama dengan persegi panjang kedua sebangun? Berikan alasannya! 2. Apakah persegi panjang pertama dengan persegi panjang ketiga sebangun? Berikan alasannya! 3. Apakah persegi panjang kedua dengan persegi panjang ketiga sebangun? Berikan alasannya!
Berdasarkan gambar tersebut, jawablah pertanyaan berikut ini:
1. Apakah persegi panjang pertama dengan persegi panjang kedua sebangun? Berikan alasannya!
2. Apakah persegi panjang pertama dengan persegi panjang ketiga sebangun? Berikan alasannya!
3. Apakah persegi panjang kedua dengan persegi panjang ketiga sebangun? Berikan alasannya!
2
2
Iklan
N. A

Community
19 Januari 2024 07:08
<p>Jawaban yang tepat untuk pertanyaan nomor 1, 2, dan 3 secara berturut-turut adalah <strong>sebangun, tidak sebangun, dan tidak sebangun</strong>.</p><p> </p><p><strong>Penjelasan:</strong></p><p>Sepasang bangun datar dikatakan sebangun apabila <strong>semua</strong> perbandingan sisi terhadap sisi yang bersesuaian tempatnya di bangun datar pasangannya<strong> sama</strong>. Serta, <strong>semua</strong> besar sudut <strong>sama</strong> dengan besar sudut di bangun datar pasangannya yang tempatnya bersesuaian.</p><p> </p><p>Dalam soal nomor 1, kita diminta untuk menentukan apakah persegi panjang yang pertama sebangun dengan persegi panjang kedua. Untuk itu, kita bisa mengecek apakah perbandingan panjangnya sama dengan perbandingan lebarnya. Harap diketahui bahwa persegi panjang kedua terotasi 90°, jadi panjang sisi kanan di persegi panjang kedua adalah panjangnya, sementara panjang sisi atas adalah lebarnya.</p><p>Setelah itu, kita bisa mengecek perbandingan panjang dan lebarnya. Karena panjang dan lebar persegi panjang pertama secara berturut-turut adalah 6 dan 4, sementara di persegi panjang kedua adalah 3 dan 2, maka jika sebangun, 6/4 <strong>harus</strong> <strong>=</strong> 3/2. Karena 6/4 = 3/2, maka persegi panjang pertama <strong>sebangun</strong> dengan persegi panjang kedua.</p><p> </p><p>Lanjut, kita ingin cek kesebangunan antara persegi panjang yang pertama dengan yang ketiga. Karena tampaknya persegi panjang yang ketiga juga dirotasi 90°, maka panjang dan lebar ditukar. Setelah itu, cek apakah 6/4 = 4/3. Ternyata, 6/4 <strong>≠</strong> 4/3, jadi persegi panjang pertama <strong>tidak sebangun</strong> dengan persegi panjang ketiga.</p><p> </p><p>Setelah itu, kita bahas pertanyaan nomor 3. Sebenarnya dari hal yang diketahui saja, kita sudah bisa mengatakan bahwa persegi panjang kedua <strong>tidak sebangun</strong> dengan persegi panjang ketiga. Karena persegi panjang pertama tidak sebangun dengan persegi panjang ketiga. Hal ini disebabkan oleh prinsip yang seperti "Jika a = b dan b = c, maka a = c. Jika a = b dan b ≠ c, maka a ≠ c". Ini juga berlaku untuk kesebangunan, maka kita sudah bisa putuskan bahwa persegi panjang kedua <strong>tidak sebangun</strong> dengan persegi panjang ketiga.</p><p> </p><p><strong>Jadi, persegi panjang pertama <u>sebangun</u> dengan persegi panjang kedua, namun persegi panjang pertama <u>tidak sebangun</u> dengan persegi panjang ketiga. Karena demikian, maka persegi panjang kedua juga <u>tidak sebangun</u> dengan persegi panjang ketiga.</strong></p>
Jawaban yang tepat untuk pertanyaan nomor 1, 2, dan 3 secara berturut-turut adalah sebangun, tidak sebangun, dan tidak sebangun.
Penjelasan:
Sepasang bangun datar dikatakan sebangun apabila semua perbandingan sisi terhadap sisi yang bersesuaian tempatnya di bangun datar pasangannya sama. Serta, semua besar sudut sama dengan besar sudut di bangun datar pasangannya yang tempatnya bersesuaian.
Dalam soal nomor 1, kita diminta untuk menentukan apakah persegi panjang yang pertama sebangun dengan persegi panjang kedua. Untuk itu, kita bisa mengecek apakah perbandingan panjangnya sama dengan perbandingan lebarnya. Harap diketahui bahwa persegi panjang kedua terotasi 90°, jadi panjang sisi kanan di persegi panjang kedua adalah panjangnya, sementara panjang sisi atas adalah lebarnya.
Setelah itu, kita bisa mengecek perbandingan panjang dan lebarnya. Karena panjang dan lebar persegi panjang pertama secara berturut-turut adalah 6 dan 4, sementara di persegi panjang kedua adalah 3 dan 2, maka jika sebangun, 6/4 harus = 3/2. Karena 6/4 = 3/2, maka persegi panjang pertama sebangun dengan persegi panjang kedua.
Lanjut, kita ingin cek kesebangunan antara persegi panjang yang pertama dengan yang ketiga. Karena tampaknya persegi panjang yang ketiga juga dirotasi 90°, maka panjang dan lebar ditukar. Setelah itu, cek apakah 6/4 = 4/3. Ternyata, 6/4 ≠ 4/3, jadi persegi panjang pertama tidak sebangun dengan persegi panjang ketiga.
Setelah itu, kita bahas pertanyaan nomor 3. Sebenarnya dari hal yang diketahui saja, kita sudah bisa mengatakan bahwa persegi panjang kedua tidak sebangun dengan persegi panjang ketiga. Karena persegi panjang pertama tidak sebangun dengan persegi panjang ketiga. Hal ini disebabkan oleh prinsip yang seperti "Jika a = b dan b = c, maka a = c. Jika a = b dan b ≠ c, maka a ≠ c". Ini juga berlaku untuk kesebangunan, maka kita sudah bisa putuskan bahwa persegi panjang kedua tidak sebangun dengan persegi panjang ketiga.
Jadi, persegi panjang pertama sebangun dengan persegi panjang kedua, namun persegi panjang pertama tidak sebangun dengan persegi panjang ketiga. Karena demikian, maka persegi panjang kedua juga tidak sebangun dengan persegi panjang ketiga.
· 0.0 (0)
Iklan
Albert A
19 Januari 2024 12:51
<p>Untuk persegi panjang yang pertama, kedua, dan ketiga tidak sebangun</p>
Untuk persegi panjang yang pertama, kedua, dan ketiga tidak sebangun
· 0.0 (0)
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



