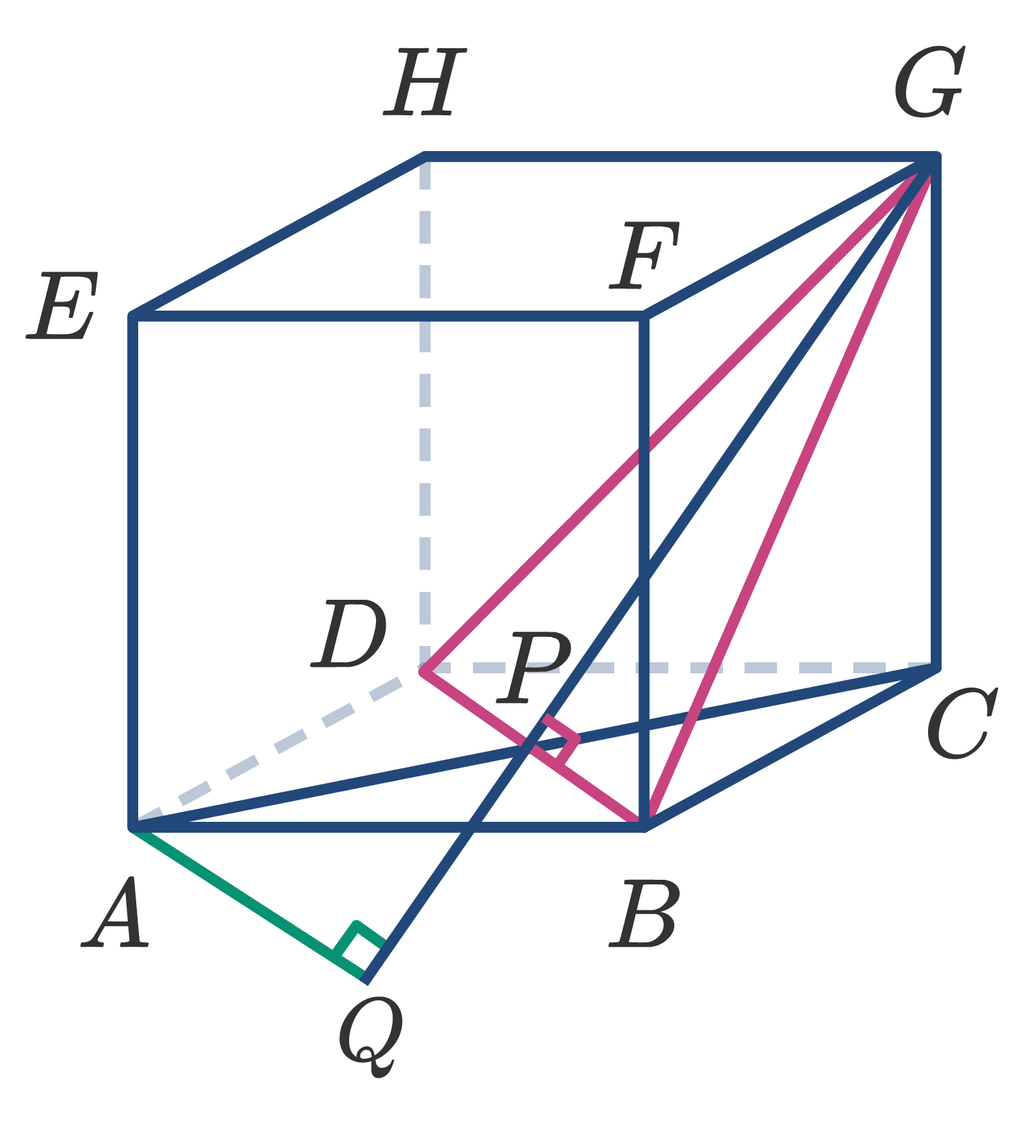
ABCD.EFGH adalah sebuah kubus dengan panjang rusuk 3a cm. Jarak A ke bidang BDG sama dengan .... A. (a/3)√6 cm D. a√3 cm B. (a/2)√6 cm E. a√6 cm C. (a/3)√3cm

Question

Jawaban: D

Ingat konsep berikut ini:

diagonal bidang = rusuk √2

sin α = sisi depan/sisi miring

Gambar terlampir di bawah

Jarak A ke BDG = AG
Pada ABDG sama sisi, GP garis tinggi maka GP garis berat. P terletak di tengah BD

AC = diagonal bidang
AC = rusuk √2
AC = 3a√2
PC = AP
AP = (1/2) . AC
AP = (1/2) (3a√2)
AP = (3/2)a√2

GP = √(PC² + CG²)
GP = √(((3/2)a√2)² + (3a)²)
GP = √((9/4)2a² + 9a²)
GP = √((9/2)a² + (18/2)a²)
GP = √(27/2)a²
GP = √(9a² . (3/2))
GP = √(9a²) . √(3/2)
GP = 3a . (√3)/(√2)
GP = 3a . (√3)/(√2) . (√2)/(√2)
GP = 3a . (√6)/(2)
GP = (3a)/(2) √6 cm

Pada segitiga PCG
sin α = CG/GP
sin α = 3a/(3/2)a √6
sin α = (2)/(√6)

Pada segitiga APQ
sin α = (AQ)/(AP)
(2)/(√6) = (AQ)/((3/2)a√2)
((3/2)a√2) . (2)/(√6) = AQ
3a . (√2/6) = AQ
3a . (√1/3) = AQ
3a . (√1)/√3) = AQ
AQ = 3a . (1)/(√3) . (√3)/(√3)
AQ = (3a)/(3) √3
AQ = a√3
Jadi, jarak A ke BDG adalah a√3 cm.

Oleh karena itu, jawaban yang tepat adalah D.

ABCD.EFGH adalah sebuah kubus dengan panjang rusuk 3a cm. Jarak A ke bidang BDG sama dengan .... A. (a/3)√6 cm D. a√3 cm B. (a/2)√6 cm E. a√6 cm C. (a/3)√3cm

Mau pemahaman lebih dalam untuk soal ini?

Pertanyaan serupa