Laila A
05 Agustus 2024 03:41
Iklan
Laila A
05 Agustus 2024 03:41
Pertanyaan
2. Diketahui garis y = kx + 1 dan lingkaran L equiv (x - 1) ^ 2 + (y + 1) ^ 2 = 4 . Tentukan syarat k agar garis y tidak memotong lingkaran L!
2. Diketahui garis y = kx + 1 dan lingkaran L equiv (x - 1) ^ 2 + (y + 1) ^ 2 = 4 . Tentukan syarat k agar garis y tidak memotong lingkaran L!
14
2
Iklan
Samudra A

Community
05 Agustus 2024 04:09
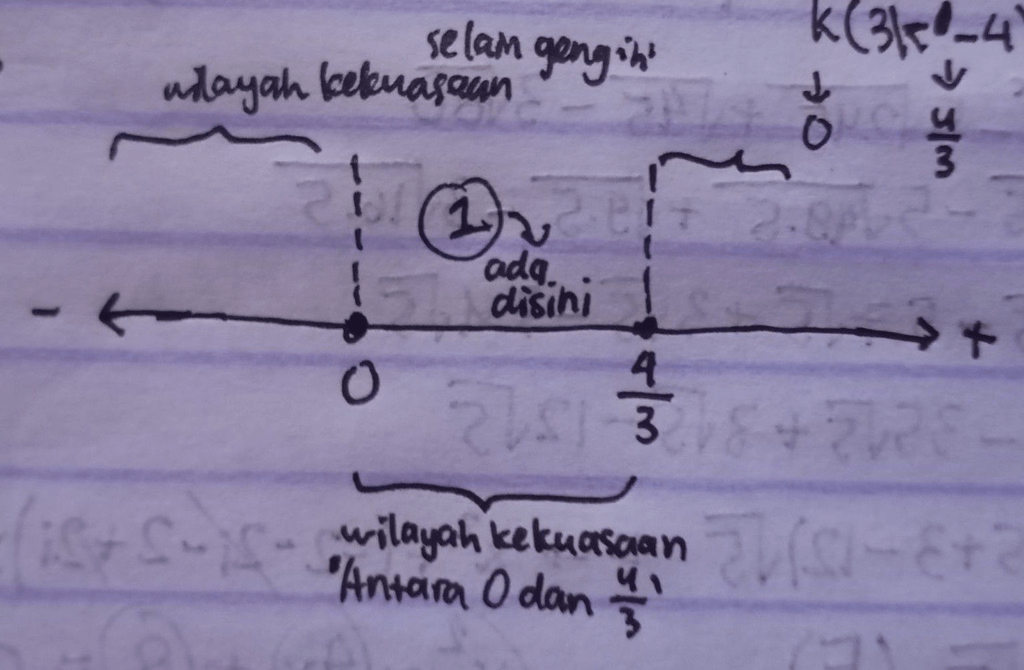
<p>kok bisa langsung meyimpulkan klo k itu antara 0 dan 4/3?</p><p> </p><p>Kan kita udah tahu kalau patokan nilai k itu ada 0 dan 4/3, nah biar tahu lebih pasti, kita gampangnya make cara ngetes aja. </p><p>Misal kita pilih untui k = 1 (1 ini kan ada di antara 0 dan 4/3) dan kita cari tahu apakah 1 ini bakal memenuhi D < 0</p><p>3k² - 4k < 0</p><p>3 - 4 < 0 (BENAR) </p><p>wah, krn ternyata 1 ini benar, artinya ia <strong>memenuhi</strong> buat jadi salah satu solusi untuk k, dan karena 1 ini termasuk di dalam geng yg namanya '<strong>Antara 0 dan 4/3</strong>', jadi keseluruhan anggota geng tsb juga pasti memenuhi (lha wong soalnya satu anggotanya bener, pasti semua anggota lain bener). </p><p>Nah klo misalkan ternyata 1 ini <strong>gk memenuhi,</strong> berarti geng 'Antara 0 dan 4/3' ini jelas gk memenuhi semua, dan solusi untuk k adalah geng bernama '<strong>Selain Antara 0 dan 4/3</strong>' (ditulis k<0 dan k>4/3) yang merupakan rival dari geng yg pertama itu. </p><p> </p><p>semoga paham ya wak</p>
kok bisa langsung meyimpulkan klo k itu antara 0 dan 4/3?
Kan kita udah tahu kalau patokan nilai k itu ada 0 dan 4/3, nah biar tahu lebih pasti, kita gampangnya make cara ngetes aja.
Misal kita pilih untui k = 1 (1 ini kan ada di antara 0 dan 4/3) dan kita cari tahu apakah 1 ini bakal memenuhi D < 0
3k² - 4k < 0
3 - 4 < 0 (BENAR)
wah, krn ternyata 1 ini benar, artinya ia memenuhi buat jadi salah satu solusi untuk k, dan karena 1 ini termasuk di dalam geng yg namanya 'Antara 0 dan 4/3', jadi keseluruhan anggota geng tsb juga pasti memenuhi (lha wong soalnya satu anggotanya bener, pasti semua anggota lain bener).
Nah klo misalkan ternyata 1 ini gk memenuhi, berarti geng 'Antara 0 dan 4/3' ini jelas gk memenuhi semua, dan solusi untuk k adalah geng bernama 'Selain Antara 0 dan 4/3' (ditulis k<0 dan k>4/3) yang merupakan rival dari geng yg pertama itu.
semoga paham ya wak

· 0.0 (0)
Iklan
Diannisa N
05 Agustus 2024 04:15
<p>Untuk menentukan syarat \( k \) agar garis \( y = kx + 1 \) tidak memotong lingkaran \( L \) yang memiliki persamaan \((x - 1)^2 + (y + 1)^2 = 4\), kita perlu memastikan bahwa jarak terpendek dari pusat lingkaran ke garis lebih besar dari jari-jari lingkaran.</p><p>Lingkaran \( L \) memiliki pusat di \((1, -1)\) dan jari-jari \( r = 2 \).</p><p>Pertama, kita hitung jarak dari titik \((1, -1)\) ke garis \( y = kx + 1 \). Persamaan umum garis adalah \( kx - y + 1 = 0 \). Rumus jarak dari titik \((x_1, y_1)\) ke garis \( Ax + By + C = 0 \) adalah:</p><p>\[ d = \frac{|Ax_1 + By_1 + C|}{\sqrt{A^2 + B^2}} \]</p><p>Dengan \( A = k \), \( B = -1 \), \( C = 1 \), \( x_1 = 1 \), dan \( y_1 = -1 \), kita substitusi nilai-nilai ini ke dalam rumus jarak:</p><p>\[ d = \frac{|k(1) - 1(-1) + 1|}{\sqrt{k^2 + (-1)^2}} = \frac{|k + 1 + 1|}{\sqrt{k^2 + 1}} = \frac{|k + 2|}{\sqrt{k^2 + 1}} \]</p><p>Agar garis tidak memotong lingkaran, jarak \( d \) harus lebih besar dari jari-jari lingkaran, yaitu 2:</p><p>\[ \frac{|k + 2|}{\sqrt{k^2 + 1}} > 2 \]</p><p>Kita kuadratkan kedua sisi:</p><p>\[ \frac{(k + 2)^2}{k^2 + 1} > 4 \]</p><p>Lalu kalikan kedua sisi dengan \( k^2 + 1 \):</p><p>\[ (k + 2)^2 > 4(k^2 + 1) \]</p><p>Ekspansi dan penyederhanaan:</p><p>\[ k^2 + 4k + 4 > 4k^2 + 4 \]</p><p>\[ k^2 + 4k + 4 > 4k^2 + 4 \]</p><p>\[ k^2 + 4k + 4 > 4k^2 + 4 \]</p><p>\[ k^2 + 4k + 4 - 4k^2 - 4 > 0 \]</p><p>\[ -3k^2 + 4k > 0 \]</p><p>\[ k(-3k + 4) > 0 \]</p><p>Solusi dari persamaan di atas adalah:</p><p>1. \( k > 0 \)<br>2. \( -3k + 4 > 0 \) atau \( k < \frac{4}{3} \)</p><p>Gabungan dari kedua syarat tersebut:</p><p>\[ 0 < k < \frac{4}{3} \]</p><p>Jadi, agar garis \( y = kx + 1 \) tidak memotong lingkaran \( L \), nilai \( k \) harus memenuhi syarat:</p><p>\[ 0 < k < \frac{4}{3} \]</p>
Untuk menentukan syarat \( k \) agar garis \( y = kx + 1 \) tidak memotong lingkaran \( L \) yang memiliki persamaan \((x - 1)^2 + (y + 1)^2 = 4\), kita perlu memastikan bahwa jarak terpendek dari pusat lingkaran ke garis lebih besar dari jari-jari lingkaran.
Lingkaran \( L \) memiliki pusat di \((1, -1)\) dan jari-jari \( r = 2 \).
Pertama, kita hitung jarak dari titik \((1, -1)\) ke garis \( y = kx + 1 \). Persamaan umum garis adalah \( kx - y + 1 = 0 \). Rumus jarak dari titik \((x_1, y_1)\) ke garis \( Ax + By + C = 0 \) adalah:
\[ d = \frac{|Ax_1 + By_1 + C|}{\sqrt{A^2 + B^2}} \]
Dengan \( A = k \), \( B = -1 \), \( C = 1 \), \( x_1 = 1 \), dan \( y_1 = -1 \), kita substitusi nilai-nilai ini ke dalam rumus jarak:
\[ d = \frac{|k(1) - 1(-1) + 1|}{\sqrt{k^2 + (-1)^2}} = \frac{|k + 1 + 1|}{\sqrt{k^2 + 1}} = \frac{|k + 2|}{\sqrt{k^2 + 1}} \]
Agar garis tidak memotong lingkaran, jarak \( d \) harus lebih besar dari jari-jari lingkaran, yaitu 2:
\[ \frac{|k + 2|}{\sqrt{k^2 + 1}} > 2 \]
Kita kuadratkan kedua sisi:
\[ \frac{(k + 2)^2}{k^2 + 1} > 4 \]
Lalu kalikan kedua sisi dengan \( k^2 + 1 \):
\[ (k + 2)^2 > 4(k^2 + 1) \]
Ekspansi dan penyederhanaan:
\[ k^2 + 4k + 4 > 4k^2 + 4 \]
\[ k^2 + 4k + 4 > 4k^2 + 4 \]
\[ k^2 + 4k + 4 > 4k^2 + 4 \]
\[ k^2 + 4k + 4 - 4k^2 - 4 > 0 \]
\[ -3k^2 + 4k > 0 \]
\[ k(-3k + 4) > 0 \]
Solusi dari persamaan di atas adalah:
1. \( k > 0 \)
2. \( -3k + 4 > 0 \) atau \( k < \frac{4}{3} \)
Gabungan dari kedua syarat tersebut:
\[ 0 < k < \frac{4}{3} \]
Jadi, agar garis \( y = kx + 1 \) tidak memotong lingkaran \( L \), nilai \( k \) harus memenuhi syarat:
\[ 0 < k < \frac{4}{3} \]
· 0.0 (0)
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



