Almira D
02 Agustus 2022 09:52
Iklan
Almira D
02 Agustus 2022 09:52
Pertanyaan
Tentukan daerah penyelesaian dari sistem pertidaksamaan berikut. y=x^(2)+4x-5 y=-x^(2)-3x+4
1
1
Iklan
D. Nuryani
Mahasiswa/Alumni Universitas Padjadjaran
07 November 2022 06:05
<p>Jawaban : {(x,y) | (-9/2, -2 3/4) dan (1,0)}</p><p> </p><p>Asumsikan maksud soal adalah untuk mencari nilai x, y dari sistem persamaan y=x^(2)+4x-5, y=-x^(2)-3x+4.</p><p> </p><p>Langkah menggambar fungsi kuadrat y = ax² + bx + c :<br>1. Menentukan titik potong sumbu X, y = 0<br>2. Menentukan titik potong sumbu Y, x = 0<br>3. Menentukan titik puncak (xp, yp) = (-b/2a, (b² - 4ac)/-4a)<br>3. Hubungkan titik-titik yang telah didapat</p><p> </p><p>▪️ y=x^(2)+4x-5</p><p>a = 1, b = 4, c = -5</p><p> </p><p>➡️ Titik potong sumbu X, y = 0</p><p>x^(2)+4x-5 = 0</p><p>(x - 1)(x + 5) = 0</p><p>x = 1 atau x = -5</p><p>(1, 0) dan (-5, 0)</p><p> </p><p>➡️ Titik potong sumbu Y, x = 0</p><p>y = 0^(2)+4(0)-5</p><p>y = -5</p><p>(0, -5)</p><p> </p><p>➡️ Titik puncak</p><p>(xp, yp) = (-b/2a, (b² - 4ac)/-4a)</p><p>= (-4/2(1), (4^2 - 4(1)(-5))/-4(1))</p><p>= (-2, 36/(-4))</p><p>= (-2, -9)</p><p> </p><p>▪️ y=-x^(2)-3x+4</p><p>a = -1, b = -3, c = 4</p><p> </p><p>➡️ Titik potong sumbu X, y = 0</p><p>-x^(2)-3x+4 = 0</p><p>(-x+1)(x+4) = 0</p><p>-x = -1 atau x = -4</p><p>x = 1 atau x = -4</p><p>(1, 0) dan (-4, 0)</p><p> </p><p>➡️ Titik potong sumbu Y, x = 0</p><p>y = -0^(2)-3(0)+4</p><p>y = 4</p><p>(0, 4)</p><p> </p><p>➡️ Titik puncak</p><p>(xp, yp) = (-b/2a, (b² - 4ac)/-4a)</p><p>= (3/2(-1), ((-3)^2 - 4(-1)(4))/-4(-1))</p><p>= (-3/2, 25/4)</p><p> </p><p>Gambarkan kedua grafik pada bidang kartesius, kemudian cari titik potong kedua grafik.</p><p> </p><p>Dari gambar, titik poyong kedua grafik adalah di titik (-9/2, -2 3/4) dan di titik (1,0).</p><p> </p><p>Jadi, Himpunan Penyelesaiannya adalah {(x,y) | (-9/2, -2 3/4) dan (1,0)}.</p>
Jawaban : {(x,y) | (-9/2, -2 3/4) dan (1,0)}
Asumsikan maksud soal adalah untuk mencari nilai x, y dari sistem persamaan y=x^(2)+4x-5, y=-x^(2)-3x+4.
Langkah menggambar fungsi kuadrat y = ax² + bx + c :
1. Menentukan titik potong sumbu X, y = 0
2. Menentukan titik potong sumbu Y, x = 0
3. Menentukan titik puncak (xp, yp) = (-b/2a, (b² - 4ac)/-4a)
3. Hubungkan titik-titik yang telah didapat
▪️ y=x^(2)+4x-5
a = 1, b = 4, c = -5
➡️ Titik potong sumbu X, y = 0
x^(2)+4x-5 = 0
(x - 1)(x + 5) = 0
x = 1 atau x = -5
(1, 0) dan (-5, 0)
➡️ Titik potong sumbu Y, x = 0
y = 0^(2)+4(0)-5
y = -5
(0, -5)
➡️ Titik puncak
(xp, yp) = (-b/2a, (b² - 4ac)/-4a)
= (-4/2(1), (4^2 - 4(1)(-5))/-4(1))
= (-2, 36/(-4))
= (-2, -9)
▪️ y=-x^(2)-3x+4
a = -1, b = -3, c = 4
➡️ Titik potong sumbu X, y = 0
-x^(2)-3x+4 = 0
(-x+1)(x+4) = 0
-x = -1 atau x = -4
x = 1 atau x = -4
(1, 0) dan (-4, 0)
➡️ Titik potong sumbu Y, x = 0
y = -0^(2)-3(0)+4
y = 4
(0, 4)
➡️ Titik puncak
(xp, yp) = (-b/2a, (b² - 4ac)/-4a)
= (3/2(-1), ((-3)^2 - 4(-1)(4))/-4(-1))
= (-3/2, 25/4)
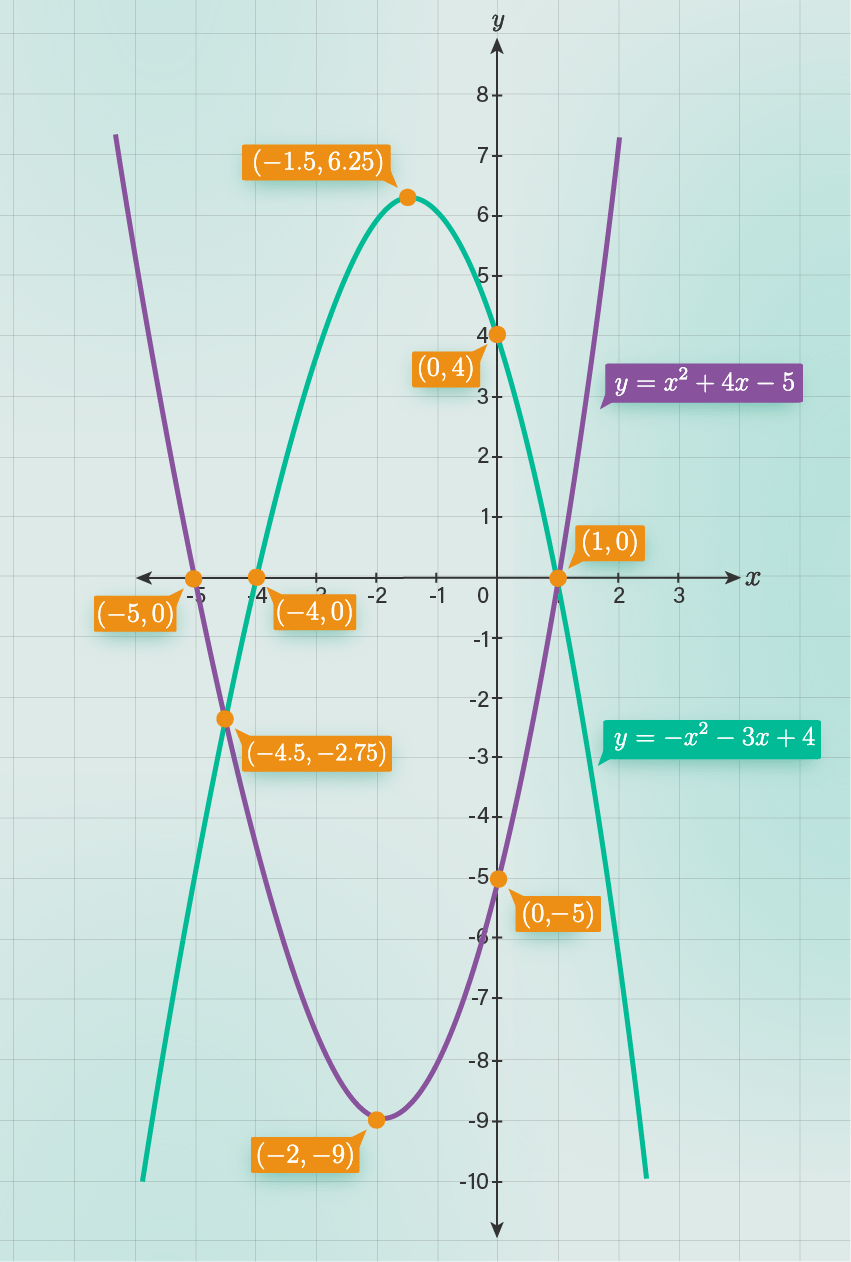
Gambarkan kedua grafik pada bidang kartesius, kemudian cari titik potong kedua grafik.
Dari gambar, titik poyong kedua grafik adalah di titik (-9/2, -2 3/4) dan di titik (1,0).
Jadi, Himpunan Penyelesaiannya adalah {(x,y) | (-9/2, -2 3/4) dan (1,0)}.
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke Forum
Biar Robosquad lain yang jawab soal kamu

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



