Aulia R
15 Januari 2023 04:15
Iklan
Aulia R
15 Januari 2023 04:15
Pertanyaan
Seorang pedagang roti keliling menjual roti cokelat dan roti pisang. Roti cokelat dibeli dari agen seharga Rp4.000,00 dan dijualnya Rp7.500,00 per buah, sedangkan roti pisang dibeli seharga Rp2.000,00 dan dijualnya Rp4.000,00 per buah. Pedagang tersebut memiliki uang Rp400.000,00 dan ia bermaksud untuk membeli kedua jenis roti tersebut. Akan tetapi, karena keterbatasan tempat, ia tidak mau membeli kedua jenis roti tersebut lebih dari 100 buah. d. Berapa keuntungan maksimum yang bisa diperoleh dari kedua jenis roti tersebut dan berapa kotak roti cokelat dan roti pisang yang harus dibelinya agar mendapatkan keuntungan maksimum?
1
1
Iklan
P. Vidya
Mahasiswa/Alumni Universitas Negeri Malang
27 Maret 2023 03:31
<p>Halo Keysha. Kakak bantu jawab ya.</p><p>Jawab: Jadi, jawaban yang benar adalah keuntungan maksimum Rp350.000,00 dengan 100 roti cokelat dan 0 roti pisang. </p><p>Pembahasan:</p><p>Misal x adalah banyak roti cokelat dan y adalah banyak roti pisang.</p><p><u>Langkah 1. Menentukan sistem pertidaksamaan dan fungsi tujuan.</u></p><ul><li>Karena harga beli roti cokelat perbuah adalah Rp4.000,00 dan harga beli roti pisang perbuah adalah Rp2.000,00, serta pedagang memiliki uang Rp400.000,00, maka pertidaksamaan matematikanya adalah </li></ul><p> 4000x+2000y ≤ 400.000</p><p> 2x+y ≤ 200</p><ul><li>Karena pedagang tidak mau membeli roti lebih dari 100 buah, maka pertidaksamaan matematikanya adalah</li></ul><p> x+y ≤ 100</p><ul><li>Banyak roti cokelat dan banyak roti pisang selalu bernilai lebih dari atau sama dengan nol, maka pertidaksamaannya adalah x≥0 dan y≥0.</li><li>Fungsi tujuannya adalah memaksimalkan keuntungan.</li></ul><p>Menentukan keuntungan yang diperoleh untuk satu buah roti cokelat.</p><p>Keuntungan = Harga jual-harga beli</p><p> = 7.500 - 4.000</p><p> = 3.500</p><p>Menentukan keuntungan yang diperoleh untuk satu buah roti pisang.</p><p>Keuntungan = Harga jual-harga beli</p><p> = 4.000 - 2.000</p><p> = 2.000</p><p>Sehingga, fungsi tujuannya adalah memaksimalkan </p><p>F(x, y) = 3.500x+2.000y</p><p>Oleh karena itu, sistem pertidaksamaannya adalah </p><p>2x+y ≤ 200</p><p>x+y ≤ 100</p><p>x≥0 </p><p>y≥0</p><p>Fungsi tujuan F(x, y) = 3.500x+2.000y</p><p><u>Langkah 2. Menentukan daerah himpunan penyelesaian.</u></p><ul><li>Menggambar daerah penyelesaian 2x+y ≤ 200.</li></ul><p>Dari persamaan linear 2x+y = 200, </p><p>Jika x = 0 maka y = 200.</p><p>Jika y = 0 maka x = 100.</p><p>Sehingga persamaan linear 2x+y = 200 melalui titik (0, 200) dan (100, 0).</p><p>Menentukan daerah penyelesaiannya dengan melakukan uji titik, misal titik (0, 0).</p><p> 2x+y ≤ 200</p><p>2(0)+0 ≤ 200</p><p> 0 ≤ 200 (benar)</p><p>Sehingga daerah penyelesaian 2x+y ≤ 200 adalah daerah yang memuat (0, 0).</p><ul><li>Menggambar daerah penyelesaian x+y ≤ 100.</li></ul><p>Dari persamaan linear x+y = 100, </p><p>Jika x = 0 maka y = 100.</p><p>Jika y = 0 maka x = 100.</p><p>Sehingga persamaan linear x+y =100 melalui titik (0,100) dan (100,0).</p><p>Menentukan daerah penyelesaiannya dengan melakukan uji titik, misal titik (0, 0).</p><p> x+y ≤ 100</p><p> (0)+0 ≤ 100</p><p> 0 ≤ 100 (benar)</p><p>Sehingga daerah penyelesaian x+y ≤ 100 adalah daerah yang memuat (0, 0).</p><ul><li>Karena x≥0 dan y≥0, maka daerah penyelesaian dari sistem pertidaksamaan tersebut adalah irisannya, yaitu seperti pada gambar berikut.</li></ul><p>Berdasarkan gambar tersebut, titik sudut himpunan penyelesaiannya adalah C(0, 100), B(100, 0), dan D(0, 0).</p><p><u>Langkah 3. Menentukan nilai fungsi objektif setiap titik pojok.</u></p><p>Fungsi objektifnya adalah F(x, y) = 3.500x+2.000y.</p><p>Titik C.</p><p>F(0, 100) = 3.500(0)+2.000(100)</p><p> = 0+200.000</p><p> = 200.000</p><p>Titik B.</p><p>F(100, 0) = 3.500(100)+2.000(0)</p><p> = 350.000+0</p><p> = 350.000</p><p>Titik D.</p><p>F(0, 0) = 3.500(0)+2.000(0)</p><p> = 0+0</p><p> = 0</p><p>Langkah 4. <u>Menentukan keuntungan maksimum dan banyak roti.</u></p><p>Berdasarkan langkah 3, diperoleh bahwa keuntungan maksimum adalah Rp350.000,00 dengan 100 roti cokelat dan 0 roti pisang. </p><p> </p><p><strong><u>Jadi, jawaban yang benar adalah keuntungan maksimum Rp350.000,00 dengan 100 roti cokelat dan 0 roti pisang. </u></strong></p>
Halo Keysha. Kakak bantu jawab ya.
Jawab: Jadi, jawaban yang benar adalah keuntungan maksimum Rp350.000,00 dengan 100 roti cokelat dan 0 roti pisang.
Pembahasan:
Misal x adalah banyak roti cokelat dan y adalah banyak roti pisang.
Langkah 1. Menentukan sistem pertidaksamaan dan fungsi tujuan.
- Karena harga beli roti cokelat perbuah adalah Rp4.000,00 dan harga beli roti pisang perbuah adalah Rp2.000,00, serta pedagang memiliki uang Rp400.000,00, maka pertidaksamaan matematikanya adalah
4000x+2000y ≤ 400.000
2x+y ≤ 200
- Karena pedagang tidak mau membeli roti lebih dari 100 buah, maka pertidaksamaan matematikanya adalah
x+y ≤ 100
- Banyak roti cokelat dan banyak roti pisang selalu bernilai lebih dari atau sama dengan nol, maka pertidaksamaannya adalah x≥0 dan y≥0.
- Fungsi tujuannya adalah memaksimalkan keuntungan.
Menentukan keuntungan yang diperoleh untuk satu buah roti cokelat.
Keuntungan = Harga jual-harga beli
= 7.500 - 4.000
= 3.500
Menentukan keuntungan yang diperoleh untuk satu buah roti pisang.
Keuntungan = Harga jual-harga beli
= 4.000 - 2.000
= 2.000
Sehingga, fungsi tujuannya adalah memaksimalkan
F(x, y) = 3.500x+2.000y
Oleh karena itu, sistem pertidaksamaannya adalah
2x+y ≤ 200
x+y ≤ 100
x≥0
y≥0
Fungsi tujuan F(x, y) = 3.500x+2.000y
Langkah 2. Menentukan daerah himpunan penyelesaian.
- Menggambar daerah penyelesaian 2x+y ≤ 200.
Dari persamaan linear 2x+y = 200,
Jika x = 0 maka y = 200.
Jika y = 0 maka x = 100.
Sehingga persamaan linear 2x+y = 200 melalui titik (0, 200) dan (100, 0).
Menentukan daerah penyelesaiannya dengan melakukan uji titik, misal titik (0, 0).
2x+y ≤ 200
2(0)+0 ≤ 200
0 ≤ 200 (benar)
Sehingga daerah penyelesaian 2x+y ≤ 200 adalah daerah yang memuat (0, 0).
- Menggambar daerah penyelesaian x+y ≤ 100.
Dari persamaan linear x+y = 100,
Jika x = 0 maka y = 100.
Jika y = 0 maka x = 100.
Sehingga persamaan linear x+y =100 melalui titik (0,100) dan (100,0).
Menentukan daerah penyelesaiannya dengan melakukan uji titik, misal titik (0, 0).
x+y ≤ 100
(0)+0 ≤ 100
0 ≤ 100 (benar)
Sehingga daerah penyelesaian x+y ≤ 100 adalah daerah yang memuat (0, 0).
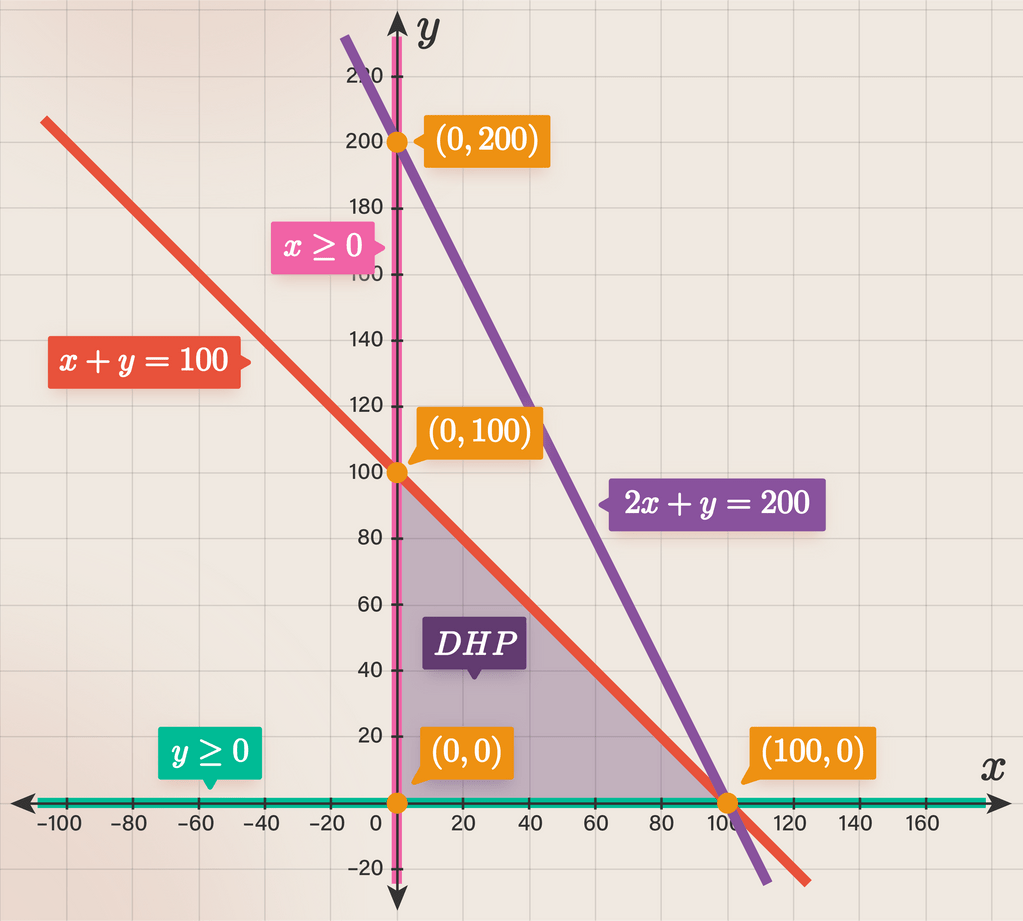
- Karena x≥0 dan y≥0, maka daerah penyelesaian dari sistem pertidaksamaan tersebut adalah irisannya, yaitu seperti pada gambar berikut.
Berdasarkan gambar tersebut, titik sudut himpunan penyelesaiannya adalah C(0, 100), B(100, 0), dan D(0, 0).
Langkah 3. Menentukan nilai fungsi objektif setiap titik pojok.
Fungsi objektifnya adalah F(x, y) = 3.500x+2.000y.
Titik C.
F(0, 100) = 3.500(0)+2.000(100)
= 0+200.000
= 200.000
Titik B.
F(100, 0) = 3.500(100)+2.000(0)
= 350.000+0
= 350.000
Titik D.
F(0, 0) = 3.500(0)+2.000(0)
= 0+0
= 0
Langkah 4. Menentukan keuntungan maksimum dan banyak roti.
Berdasarkan langkah 3, diperoleh bahwa keuntungan maksimum adalah Rp350.000,00 dengan 100 roti cokelat dan 0 roti pisang.
Jadi, jawaban yang benar adalah keuntungan maksimum Rp350.000,00 dengan 100 roti cokelat dan 0 roti pisang.
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



