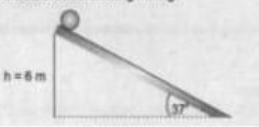
Sebuah silinder tipis berongga yang massanya 1 kg dan berjari-jari 30 cm menggelinding dari puncak bidang miring seperti pada gambar berikut. Hitunglah kecepatan silinder saat berada di dasar bidang miring!

<p>Jawaban yang benar adalah 2√15 m/s.</p><p>&nbsp;</p><p>Diketahui:</p><p>Silinder tipis berongga (I = m R²) menggelinding di atas bidang miring sampai dasar</p><p>m = 1 kg</p><p>R = 30 cm = 0,3 m</p><p>h = 6 m</p><p>θ = 37°</p><p>&nbsp;</p><p>Ditanya:</p><p>v = ...?</p><p>&nbsp;</p><p>Jawab:</p><p>Konsep yang dapat kita gunakan adalah hukum kekekalan energi. Dari gambar tersebut kita tentukan kecepatan akhir benda pada saat di dasar bidang miring (misalkan titik B) dengan hukum kekekalan energi mekanik. Misalkan titik A saat benda di puncak bidang miring, sehingga diperoleh hasil:</p><p>EMA = EMB</p><p>EPA + EK,tA + EK,rA = EPB + EK,tB + EK,rB</p><p>(m x g x h) + 0 + 0 = 0 + (1/2 x m x v²) + (1/2 x I x ω²)</p><p>m x g x h = (1/2 x m x v²) + (1/2 x (k x m x R²) x ω²)</p><p>m x g x h = (1/2 x m x v²) + (1/2 x k x m x v²)</p><p>g x h = 1/2 x v² x (1 + k)</p><p>v² = 2 x g x h / (1 + k)</p><p>v = √[ 2 x g x h / (1 + k)].</p><p>&nbsp;</p><p>Substitusi nilai yang diperoleh pada soal ke rumus di atas, maka diperoleh hasil akhir:</p><p>v = √[ 2 x g x h / (1 + k)]</p><p>v = √[ 2 x 10 x 6 / (1 + 1)]</p><p>v = √[120/2]</p><p>v = √60</p><p>v = 2√15 m/s.</p><p>&nbsp;</p><p>Jadi, kecepatan silinder saat berada di dasar bidang miring adalah 2√15 m/s.</p>