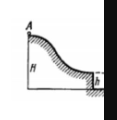
Sebuah piringan kecil a meluncur ke bawah dengan kecepatan awal sama dengan nol dari bukit licin setinggi h seperti pada gambar. Dengan memvariasikan nilai h, jarak s maksimum yang bisa dicapai ialah ... a. 2H b. H c. ¾ H d. ½ H e. ¼ H

Question

Jawaban pada soal ini adalah b

Diketahui:

H = ketinggian maksimum

h = ketinggian sebelum mencapai permukaan

s = jarak maksimum benda setelah meluncur

Ditanyakan:

s = ...?

Soal ini menggunakan hukum kekekalan energi. Hukum kekekalan energi berbunyi "energi tidak dapat diciptakan atau dimusnahkan, energi hanya dapat diubah dari satu bentuk menjadi bentuk lain."

dari ketinggian H hingga ketinggian h terjadi perubahan energi potensial. Energi potensial tersebut diubah menjadi energi kinetik sehingga diperoleh

mv²/2 = mgH - mgh

diperoleh kecepatan pada saat di h adalah

v = √2g(H-h) ...(1)

Setelah turun dari bukit, benda akan bergerak parabola dimana waktu hingga mencapai dasar permukaan diberikan sebagai

t = √2h/g ...(2)

ketika benda bergerak menuju permukaan, benda cenderung bergerak mendatar dimana pada gerak parabola, gerak dalam arah mendatar merupakan komponen gerak lurus beraturan sehingga besarnya jarak benda ketika bergerak diberikan pada rumus gerak lurus beraturan dimana

s = vt ...(3)

Persamaan (1) dan (2) disubtitusikan ke persamaan (3)

s = √2g(H-h)(√2h/g)

s = √4(H-h)h ...(4)

Mencari jarak maksimum

Agar s bernilai maksimum, maka turunan pertamanya terhadap h haruslah bernilai 0 dimana

ds/dh = 0

d(√4(H-h)h)/dh = 0

dengan menggunakan teknik diferensiasi, diperoleh

(4H-8h)(4(H-h)h)^-1/2/2 = 0

4H - 8h = 0

h = H/2 ...(5)

s bernilai maksimum apabila h = H/2. Subtitusikan persamaan (5) ke persamaan (4)

s = √4(H-h)h

s = √4(H-H/2)H/2

s = √4H²/4

s = H

Jadi, jarak s maksimum yang bisa dicapai ialah sebesar H

Sebuah piringan kecil a meluncur ke bawah dengan kecepatan awal sama dengan nol dari bukit licin setinggi h seperti pada gambar. Dengan memvariasikan nilai h, jarak s maksimum yang bisa dicapai ialah ... a. 2H b. H c. ¾ H d. ½ H e. ¼ H

Mau pemahaman lebih dalam untuk soal ini?

Pertanyaan serupa