Shesar V
06 Mei 2022 02:03
Iklan
Shesar V
06 Mei 2022 02:03
Pertanyaan
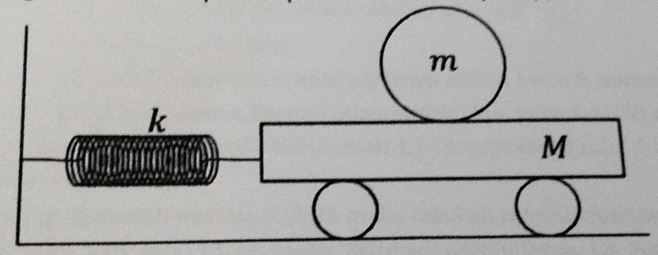
Sebuah kereta dengan massa M = 20 kg dapat bergerak bebas tanpa gesekan. Kereta ini dihubungkan ke dinding lewat sebuah pegas dengan konstanta pegas k = 700 N/m, di atas kereta terdapat bola dengan massa m = 5 kg, jari-jari r = 10 cm dan momen inersia I = 2/5 mr2. Koefisien gesekan antara bola dan kereta adalah u = 0,5. Hitunglah amplitudo maksimum osilasi (dalam cm) kereta agar bola tidak terpeleset (bola berosilasi tanpa salip)
2
1
Iklan
Y. Frando
24 September 2022 01:13
<p>Jawaban yang benar adalah 53,57 cm.</p><p> </p><p>Diketahui:</p><p>M = 20 kg</p><p>k = 700 N/m</p><p>m = 5 kg</p><p>r = 10 cm</p><p>Bola pejal, I = 2/5 m R²</p><p>μ = 0,5</p><p> </p><p>Ditanya:</p><p>x maks agar bola berosilasi tanpa slip = ...?</p><p> </p><p>Jawab:</p><p>Konsep yang kita gunakan adalah dinamika rotasi. Ketika benda tegar menggelinding, maka terdapat momen gaya yang menyebabkan benda berotasi dan sekaligus bertranslasi. Rumus yang dapat digunakan adalah hukum II Newton dan hubungan antara momen gaya dengan momen inersia.</p><p> </p><p>(a). Hukum II Newton:</p><p>ΣF = m x a.</p><p> </p><p>(b). Relasi momen gaya dengan momen inersia:</p><p>Στ = I x α ---> dimana α = a/R.</p><p> </p><p>Keterangan:</p><p>ΣF = resultan gaya (N)</p><p>m = massa benda (kg)</p><p>a = percepatan linier (m/s²)</p><p>Στ = resultan momen gaya (Nm)</p><p>I = momen inersia (kg m²)</p><p>α = percepatan sudut (rad/s²)</p><p>R = jari-jari benda (m).</p><p> </p><p>Berdasarkan gambar diagram gaya yang diberikan pada foto di bawah, diperoleh analisis sebagai berikut.</p><p> </p><p>(a). Persamaan gerak kereta:</p><p>ΣF = M . aM</p><p>f - kx = M . aM ...(1)</p><p> </p><p>(b). Percepatan bola terhadap tanah:</p><p>am = amM + aM ...(2)</p><p> </p><p>(c). Percepatan sudut bola:</p><p>αm = amM/r ...(3)</p><p> </p><p>(d). Persamaan gerak pada bola:</p><p>Translasi:</p><p>ΣF = m . am</p><p>-f = m . (amM + aM) ...(4)</p><p> </p><p>Rotasi:</p><p>Στ = I . αm</p><p>f r = I . αm ...(5)</p><p> </p><p>Selanjutnya substitusi momen inersia bola dan persamaan (3) ke persamaan (5) diperoleh:</p><p>f r = I . αm</p><p>f r = (2/5) . m . r^2 . (amM/r)</p><p>f = (2/5) . m . amM ...(6)</p><p> </p><p>Substitusi persamaan (6) ke (4) diperoleh:</p><p>-f = m . (amM + aM)</p><p>-(2/5) . m . amM = m . (amM + aM)</p><p>-(2/5) . amM = amM + aM</p><p>aM = -(7/5) . amM</p><p>amM = -(5/7) aM ...(7)</p><p> </p><p>Substitusi persamaan (7) ke (6) maka:</p><p>f = (2/5) . m . amM</p><p>f = (2/5) . m . [-(5/7) aM]</p><p>f = -(2/7) . m . aM ...(8)</p><p> </p><p>Substitusi persamaan (8) ke (1) diperoleh:</p><p>f - kx = M . aM</p><p>[-(2/7) . m . aM] - kx = M . aM</p><p>0 = [(2/7) m aM] + kx + [M aM]</p><p>0 = aM + [7k/(2m+7M)]x ...(9)</p><p> </p><p>Selanjutnya syarat yang harus dipenuhi ketika bola tergelincir adalah:</p><p>f = μmg ...(10)</p><p> </p><p>Dari persamaan (8) dan (10) diperoleh percepatan maksimum tanpa slip yaitu:</p><p>μmg = -(2/7) . m . aM</p><p>aM = -(7/2) μg ...(11)</p><p> </p><p>Maka, dari persamaan (9) dan (11) diperoleh amplitudo maksimum adalah:</p><p>0 = aM + [7k/(2m+7M)]x</p><p>0 = -(7/2) μg + [7k/(2m+7M)]x maks</p><p>(7/2) μg = [7k/(2m+7M)]x maks</p><p>x maks = [(2m+7M) μg] / (2k).</p><p> </p><p>Substitusikan data pada soal ke persamaan x maks di atas sehingga diperoleh:</p><p>x maks = [(2m+7M) μg] / (2k)</p><p>x maks = [(2.5 + 7.20) . 0,5 . 10] / (2 . 700)</p><p>x maks = [(10 + 140) . 5] / 1.400</p><p>x maks = 15/28 m</p><p>x maks = 53,57 cm.</p><p> </p><p>Jadi, amplitudo maksimum osilasi kereta agar bola tidak terpeleset adalah 53,57 cm.</p>
Jawaban yang benar adalah 53,57 cm.
Diketahui:
M = 20 kg
k = 700 N/m
m = 5 kg
r = 10 cm
Bola pejal, I = 2/5 m R²
μ = 0,5
Ditanya:
x maks agar bola berosilasi tanpa slip = ...?
Jawab:
Konsep yang kita gunakan adalah dinamika rotasi. Ketika benda tegar menggelinding, maka terdapat momen gaya yang menyebabkan benda berotasi dan sekaligus bertranslasi. Rumus yang dapat digunakan adalah hukum II Newton dan hubungan antara momen gaya dengan momen inersia.
(a). Hukum II Newton:
ΣF = m x a.
(b). Relasi momen gaya dengan momen inersia:
Στ = I x α ---> dimana α = a/R.
Keterangan:
ΣF = resultan gaya (N)
m = massa benda (kg)
a = percepatan linier (m/s²)
Στ = resultan momen gaya (Nm)
I = momen inersia (kg m²)
α = percepatan sudut (rad/s²)
R = jari-jari benda (m).
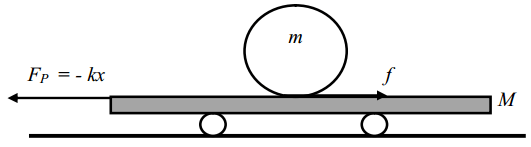
Berdasarkan gambar diagram gaya yang diberikan pada foto di bawah, diperoleh analisis sebagai berikut.
(a). Persamaan gerak kereta:
ΣF = M . aM
f - kx = M . aM ...(1)
(b). Percepatan bola terhadap tanah:
am = amM + aM ...(2)
(c). Percepatan sudut bola:
αm = amM/r ...(3)
(d). Persamaan gerak pada bola:
Translasi:
ΣF = m . am
-f = m . (amM + aM) ...(4)
Rotasi:
Στ = I . αm
f r = I . αm ...(5)
Selanjutnya substitusi momen inersia bola dan persamaan (3) ke persamaan (5) diperoleh:
f r = I . αm
f r = (2/5) . m . r^2 . (amM/r)
f = (2/5) . m . amM ...(6)
Substitusi persamaan (6) ke (4) diperoleh:
-f = m . (amM + aM)
-(2/5) . m . amM = m . (amM + aM)
-(2/5) . amM = amM + aM
aM = -(7/5) . amM
amM = -(5/7) aM ...(7)
Substitusi persamaan (7) ke (6) maka:
f = (2/5) . m . amM
f = (2/5) . m . [-(5/7) aM]
f = -(2/7) . m . aM ...(8)
Substitusi persamaan (8) ke (1) diperoleh:
f - kx = M . aM
[-(2/7) . m . aM] - kx = M . aM
0 = [(2/7) m aM] + kx + [M aM]
0 = aM + [7k/(2m+7M)]x ...(9)
Selanjutnya syarat yang harus dipenuhi ketika bola tergelincir adalah:
f = μmg ...(10)
Dari persamaan (8) dan (10) diperoleh percepatan maksimum tanpa slip yaitu:
μmg = -(2/7) . m . aM
aM = -(7/2) μg ...(11)
Maka, dari persamaan (9) dan (11) diperoleh amplitudo maksimum adalah:
0 = aM + [7k/(2m+7M)]x
0 = -(7/2) μg + [7k/(2m+7M)]x maks
(7/2) μg = [7k/(2m+7M)]x maks
x maks = [(2m+7M) μg] / (2k).
Substitusikan data pada soal ke persamaan x maks di atas sehingga diperoleh:
x maks = [(2m+7M) μg] / (2k)
x maks = [(2.5 + 7.20) . 0,5 . 10] / (2 . 700)
x maks = [(10 + 140) . 5] / 1.400
x maks = 15/28 m
x maks = 53,57 cm.
Jadi, amplitudo maksimum osilasi kereta agar bola tidak terpeleset adalah 53,57 cm.
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



