Khumaira R
14 Januari 2023 02:58
Iklan
Khumaira R
14 Januari 2023 02:58
Pertanyaan
Sebuah bangun jajargenjang memiliki panjang alas yang dinyatakan dengan a=x^(2)-4x+3 dan luasnya dinyatakan dengan L=x^(2)-25. Tentukan batas nilai x agar tinggi jajargenjang tersebut selalu lebih dari nol.
19
1
Iklan
C. Salsa
Mahasiswa/Alumni Universitas Gajah Mada
06 Februari 2023 12:35
<p>Jawaban : x < -5 atau 1 < x < 3 atau x > 5. </p><p> </p><p>Ingat!<br>Luas jajar genjang = alas . tinggi</p><p>Untuk menyelesaikan pertidaksamaan kuadrat yaitu dengan mencari pembuat nol, kemudian dilakukan uji titik. </p><p> </p><p>Diketahui jajar genjang dengan</p><p>Luas = x^(2)-25</p><p>a = alas = x^(2)-4x+3</p><p> </p><p>Sehingga</p><p>Luas = alas . tinggi</p><p>(x^(2)-25) = (x^(2)-4x+3) . tinggi</p><p>(x^(2)-25)/(x^(2)-4x+3) = tinggi</p><p> </p><p>Akan dicari batas nilai x agar tinggi jajar genjang tersebut selalu lebih dari nol.</p><p>tinggi > 0</p><p>(x^(2)-25)/(x^(2)-4x+3) > 0 </p><p>((x+5)(x-5))/((x-1)(x-3)) > 0 </p><p> </p><p>Pembuat nol : </p><p>x-5 = 0 atau x-5 = 0 </p><p>x = -5 atau x = 5</p><p> </p><p>Syarat penyebut :</p><p>x ≠ 1 atau x ≠ 3</p><p> </p><p>Uji titik : </p><p>Jika x > 5, dipilih x = 6, maka ((x+5)(x-5))/((x-1)(x-3)) = ((6+5)(6-5))/((6-1)(6-3)) = 11/15 > 0 </p><p>Jika 3 < x < 5, dipilih x = 4, maka ((x+5)(x-5))/((x-1)(x-3)) = ((4+5)(4-5))/((4-1)(4-3)) = -9/3 = -3 < 0 </p><p>Jika 1 < x < 3, dipilih x = 2, maka ((x+5)(x-5))/((x-1)(x-3)) = ((2+5)(2-5))/((2-1)(2-3)) = -21/(-1) = 21 > 0 </p><p>Jika -5 < x < 1, dipilih x = -4, maka ((x+5)(x-5))/((x-1)(x-3)) = ((-4+5)(-4-5))/((-4-1)(-4-3)) = -9/35 < 0 </p><p>Jika x < -5, dipilih x = -6, maka ((x+5)(x-5))/((x-1)(x-3)) = ((-6+5)(-6-5))/((-6-1)(6-3)) = 11/21 > 0 </p><p>Karena pertidaksamaan ((x+5)(x-5))/((x-1)(x-3)) > 0, maka dipilih yang > 0. </p><p>Diperoleh x < -5 atau 1 < x < 3 atau x > 5. </p><p> </p><p>Jadi, batas nilai x agar tinggi jajar genjang tersebut selalu lebih dari nol adalah x < -5 atau 1 < x < 3 atau x > 5. </p>
Jawaban : x < -5 atau 1 < x < 3 atau x > 5.
Ingat!
Luas jajar genjang = alas . tinggi
Untuk menyelesaikan pertidaksamaan kuadrat yaitu dengan mencari pembuat nol, kemudian dilakukan uji titik.
Diketahui jajar genjang dengan
Luas = x^(2)-25
a = alas = x^(2)-4x+3
Sehingga
Luas = alas . tinggi
(x^(2)-25) = (x^(2)-4x+3) . tinggi
(x^(2)-25)/(x^(2)-4x+3) = tinggi
Akan dicari batas nilai x agar tinggi jajar genjang tersebut selalu lebih dari nol.
tinggi > 0
(x^(2)-25)/(x^(2)-4x+3) > 0
((x+5)(x-5))/((x-1)(x-3)) > 0
Pembuat nol :
x-5 = 0 atau x-5 = 0
x = -5 atau x = 5
Syarat penyebut :
x ≠ 1 atau x ≠ 3
Uji titik :
Jika x > 5, dipilih x = 6, maka ((x+5)(x-5))/((x-1)(x-3)) = ((6+5)(6-5))/((6-1)(6-3)) = 11/15 > 0
Jika 3 < x < 5, dipilih x = 4, maka ((x+5)(x-5))/((x-1)(x-3)) = ((4+5)(4-5))/((4-1)(4-3)) = -9/3 = -3 < 0
Jika 1 < x < 3, dipilih x = 2, maka ((x+5)(x-5))/((x-1)(x-3)) = ((2+5)(2-5))/((2-1)(2-3)) = -21/(-1) = 21 > 0
Jika -5 < x < 1, dipilih x = -4, maka ((x+5)(x-5))/((x-1)(x-3)) = ((-4+5)(-4-5))/((-4-1)(-4-3)) = -9/35 < 0
Jika x < -5, dipilih x = -6, maka ((x+5)(x-5))/((x-1)(x-3)) = ((-6+5)(-6-5))/((-6-1)(6-3)) = 11/21 > 0
Karena pertidaksamaan ((x+5)(x-5))/((x-1)(x-3)) > 0, maka dipilih yang > 0.
Diperoleh x < -5 atau 1 < x < 3 atau x > 5.
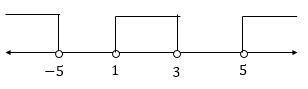
Jadi, batas nilai x agar tinggi jajar genjang tersebut selalu lebih dari nol adalah x < -5 atau 1 < x < 3 atau x > 5.
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



