Nadya S
14 Januari 2023 10:18
Iklan
Nadya S
14 Januari 2023 10:18
Pertanyaan
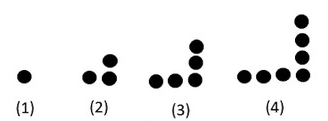
Perhatikan pola berikut! Jika pola di atas dilanjutkan, maka banyaknya bulatan pada pola ke-101 adalah... a. 197 b. 199 c. 201 d. 203
Belajar bareng Champions
Brain Academy Champions
Hanya di Brain Academy
Habis dalam
01
:
15
:
38
:
36
1
1
Iklan
M. Claudia
Mahasiswa/Alumni Universitas Nusa Cendana Kupang
01 Februari 2023 03:06
<p>Jawaban yang benar adalah C.</p><p> </p><p>Ingat!</p><p>Barisan aritmatika merupakan barisan bilangan yang memiliki selisih antara tiap suku berurutan selalu tetap (konstan). Selisih antara dua suku yang berurutan pada barisan aritmatika disebut dengan "beda" dan disimbolkan dengan b.</p><p>Rumus untuk menentukan suku ke-n dari suatu barisan aritmatika adalah:<br>U<sub>n</sub> = a + (n–1)b.<br>Keterangan:<br>Un : suku ke-n.<br>a : suku pertama barisan aritmatika.<br>b : beda → b = U<sub>n</sub> – U<sub>n-1</sub><br>n : banyaknya suku pada barisan aritmatika</p><p> </p><p>Berdasarkan soal, </p><p>pola banyaknya bulatan:</p><p>1, 3, 5, 7, ....</p><p>a = U₁ = 1<br>U₂ = 3<br>U₃ = 5</p><p>U₄ = 7</p><p>Beda antara U₁ dengan U₂<br>b = U₂ − U₁ = 3 − 1 = 2<br>Beda antara U₂ dengan U₃<br>b = U₃ − U₂ = 5 − 3 = 2<br>Beda antara U₃ dengan U₄ <br>b = U₄ − U₃ = 7 − 5 = 2</p><p>Barisan di atas membentuk barisan aritmatika karena tiap suku yang berurutan memiliki selisih yang tetap, yaitu 2.</p><p>Sehingga suku ke-101 barisan tersebut adalah sebagai berikut:</p><p>U<sub>n</sub> = a + (n–1)b</p><p>U₁₀₁ = 1 + (101–1) · 2</p><p>U₁₀₁ = 1 + 100 · 2</p><p>U₁₀₁ = 1 + 200</p><p>U₁₀₁ = 201</p><p> </p><p>Oleh karena itu, jawaban yang benar adalah C.</p><p> </p><p>Semoga membantu ya😊</p>
Jawaban yang benar adalah C.
Ingat!
Barisan aritmatika merupakan barisan bilangan yang memiliki selisih antara tiap suku berurutan selalu tetap (konstan). Selisih antara dua suku yang berurutan pada barisan aritmatika disebut dengan "beda" dan disimbolkan dengan b.
Rumus untuk menentukan suku ke-n dari suatu barisan aritmatika adalah:
Un = a + (n–1)b.
Keterangan:
Un : suku ke-n.
a : suku pertama barisan aritmatika.
b : beda → b = Un – Un-1
n : banyaknya suku pada barisan aritmatika
Berdasarkan soal,
pola banyaknya bulatan:
1, 3, 5, 7, ....
a = U₁ = 1
U₂ = 3
U₃ = 5
U₄ = 7
Beda antara U₁ dengan U₂
b = U₂ − U₁ = 3 − 1 = 2
Beda antara U₂ dengan U₃
b = U₃ − U₂ = 5 − 3 = 2
Beda antara U₃ dengan U₄
b = U₄ − U₃ = 7 − 5 = 2
Barisan di atas membentuk barisan aritmatika karena tiap suku yang berurutan memiliki selisih yang tetap, yaitu 2.
Sehingga suku ke-101 barisan tersebut adalah sebagai berikut:
Un = a + (n–1)b
U₁₀₁ = 1 + (101–1) · 2
U₁₀₁ = 1 + 100 · 2
U₁₀₁ = 1 + 200
U₁₀₁ = 201
Oleh karena itu, jawaban yang benar adalah C.
Semoga membantu ya😊
· 0.0 (0)
Iklan
Buka akses jawaban yang telah terverifikasi
Yah, akses pembahasan gratismu habis
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke Forum
Biar Robosquad lain yang jawab soal kamu
LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian
Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!
