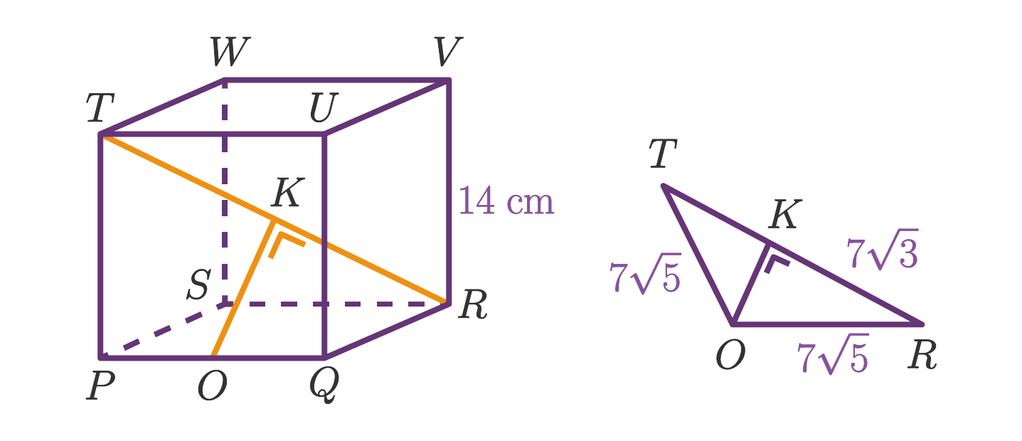
Perhatikan gambar kubus PQRS.TUVW di bawah ini! Jika panjang rusuk kubus disamping adalah 14 cm dan titik O merupakan pertengahan rusuk PQ, maka hitunglah jarak: b. Titik O ke garis RT

<p>Jawaban: 7√(2) cm.</p><p>&nbsp;</p><p>Ingat!</p><p>Kubus dengan panjang rusuk a memiliki diagonal ruang = a√(3).</p><p>&nbsp;</p><p>Perhatikan gambar di bawah ini.</p><p>Diketahui:</p><p>Kubus PQRS.TUVW dengan PQ = 14 cm</p><p>PO = 14/2 = 7 cm.</p><p>Ditanya: Jarak titik O ke garis RT.</p><p>&nbsp;</p><p>Lukis segitiga TOR, jarak titik O ke garis RT adalah panjang garis OK.</p><p>TO = √(TP²+PO²)</p><p>TO = √(14²+7²)</p><p>TO = √(196+49)</p><p>TO = √(245)</p><p>TO = √(49.5)</p><p>TO = 7√(5) cm</p><p>&nbsp;</p><p>RO = √(QR²+OQ²)</p><p>RO = √(14²+7²)</p><p>RO = √(196+49)</p><p>RO = √(245)</p><p>RO = √(49.5)</p><p>RO = 7√(5) cm</p><p>&nbsp;</p><p>TR = 14√(3) cm (TR diagonal ruang)</p><p>&nbsp;</p><p>Sehingga segitiga TOR adalah segitiga sama kaki dengan TO = OR.</p><p>Karena sama kaki, maka OK membagi TR sama panjang yaitu TK = KR = 1/2 .TR = 1/2 . 14√(3) = 7√(3) cm.</p><p>&nbsp;</p><p>Menentukan OK dengan rumus Pythagoras.</p><p>OK = √(OR²-KR²)</p><p>OK = √((7√(5))^2-(7√(3))²)</p><p>OK = √(245-147)</p><p>OK = √(98)</p><p>OK = √(49.2)</p><p>OK = 7√(2) cm</p><p>&nbsp;</p><p>Jadi, jarak titik O ke garis RT adalah 7√(2) cm.</p>