FA
Fajar A
15 Juli 2022 08:47
Iklan
FA
Fajar A
15 Juli 2022 08:47
Pertanyaan
Perhatikan gambar dibawah ini. Daerah penyelesaian dari sistem pertidaksamaan: 3x + 2y ≤ 36 x + 2y ≥ 20 x ≥ 0 y ≥ 0 Pada gambar disamping adalah... A. V B. IV C. III D. II E.I
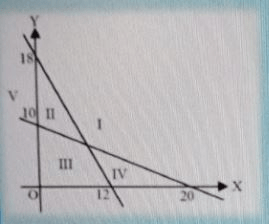
6
2
Iklan
AM
A. Meylin
Mahasiswa/Alumni Universitas Airlangga
18 Agustus 2022 03:33
Jawaban terverifikasi
Jawaban yang benar adalah D. II Ingat untuk menggambarkan grafik pertidaksamaan linear dua variabel maka langkah pertama mengubah bentuk pertidaksamaan menjadi persamaan untuk menentukan titik potong terhadap sumbu X jika y = 0 dan titik potong terhadap sumbu Y jika x = 0. Titik-titik potong yang diperoleh akan digambarkan pada koordinat kartesius. Hubungkan titik-titik potong yang diperoleh tersebut. Kemudian lakukan uji titik untuk menentukan daerah penyelesaiannya. Pembahasan : * Untuk daerah penyelesaian 3x + 2y ≤ 36 adalah sebagai berikut: 3x + 2y ≤ 36 -------> 3x + 2y = 36 - Menentukan titik potong terhadap sumbu X jika y = 0 3x + 2y = 36 3x + 2(0) = 36 3x = 36 x = 36/3 x = 12 sehingga diperoleh titik (12, 0) - Menentukan titik potong terhadap sumbu Y jika x = 0 3x + 2y = 36 3(0) + 2y = 36 2y = 36 y = 36/2 y = 18 sehingga diperoleh titik (0, 18) - Uji titik untuk menentukan daerah penyelesaian 3x + 2y ≤ 36 sebagai berikut: Misalkan x = 4, y = 6, maka 3(4) + 2(6) ≤ 36 -----> 12 + 12 ≤ 36 ------> 24 ≤ 36 (memenuhi) Misalkan x = 6, y = 10, maka 3(6) + 2(10) ≤ 36 -----> 18 + 20 ≤ 36 ------> 38 ≤ 36 (tidak memenuhi) Misalkan x = 4, y = 10, maka 3(4) + 2(10) ≤ 36 -----> 12 + 20 ≤ 36 ------> 32 ≤ 36 (memenuhi) * Untuk daerah penyelesaian x + 2y ≥ 20 adalah sebagai berikut: x + 2y ≥ 20 -------> x + 2y = 20 - Menentukan titik potong terhadap sumbu X jika y = 0 x + 2y = 20 x + 2(0) = 20 x = 20 sehingga diperoleh titik (20, 0) - Menentukan titik potong terhadap sumbu Y jika x = 0 x + 2y = 20 0 + 2y = 20 2y = 20 y = 20/2 y = 10 sehingga diperoleh titik (0, 10) - Uji titik untuk menentukan daerah penyelesaian x + 2y ≥ 20 sebagai berikut: Misalkan x = 8, y = 6, maka 8 + 2(6) ≥ 20 -----> 8 + 12 ≥ 20 ------> 20 ≥ 20 (memenuhi) Misalkan x = 4, y = 2, maka 4 + 2(2) ≥ 20 -----> 4 + 4 ≥ 20 ------> 8 ≥ 20 (tidak memenuhi) Misalkan x = 10, y = 6, maka 10 + 2(6) ≥ 20 -----> 10 + 12 ≥ 20 ------> 22 ≥ 20 (memenuhi) * Untuk daerah penyelesaian x ≥ 0 berada di sebelah kanan sumbu Y. * Untuk daerah penyelesaian y ≥ 0 berada di sebelah atas sumbu X. * Gambarkan daerah penyelesaian 3x + 2y ≤ 36, x + 2y ≥ 20, x ≥ 0, y ≥ 0 seperti gambar dibawah sehingga diperoleh daerah penyelesaiannya adalah nomor II. Jadi, gambar daerah penyelesaian pertidaksamaan tersebut adalah nomor D. II Semoga membantu ya.
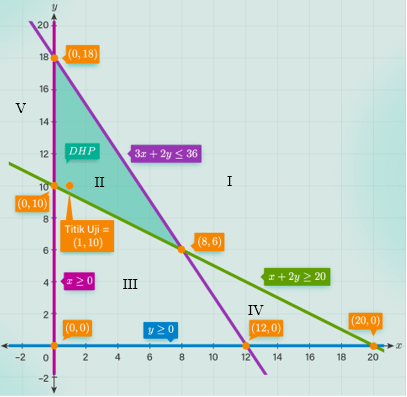
· 3.7 (3)
Iklan
JN
Jason N
04 Agustus 2023 02:29
Pertidaksamaan pertama: x + y ≤ 36 Ketika x = 0, maka y = 36. Titik potong pertama adalah (0, 36). Ketika y = 0, maka x = 36. Titik potong kedua adalah (36, 0). Pertidaksamaan kedua: x + 2y ≤ 62 Ketika x = 0, maka y = 31. Titik potong pertama adalah (0, 31). Ketika y = 0, maka x = 62. Titik potong kedua adalah (62, 0). Daerah yang memenuhi kedua pertidaksamaan tersebut berada di dalam atau pada segitiga yang dibentuk oleh garis pertidaksamaan pertama (x + y ≤ 36) dan garis pertidaksamaan kedua (x + 2y ≤ 62) serta sumbu x dan y yang non-negatif. Titik sudut segitiga: A(0, 0) - Sudut asal B(0, 31) - Titik potong pertama pertidaksamaan kedua dengan sumbu y C(34, 2) - Titik potong kedua pertidaksamaan pertama dengan sumbu x Hitung nilai fungsi objektif pada titik-titik ini: f(A) = 8(0) + 9(0) = 0 f(B) = 8(0) + 9(31) = 279 f(C) = 8(34) + 9(2) = 298 Nilai terkecil dari f(x, y) adalah 279 pada titik B (0, 31). Jadi, nilai minimum dari fungsi objektif f(x, y) = 8x + 9y dalam daerah penyelesaian sistem pertidaksamaan ini adalah 279 yang terjadi ketika x = 0 dan y = 3
· 0.0 (0)
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



