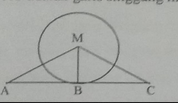
Perhatikan gambar di bawah ini! AC adalah garis singgung lingkaran M dengan titik singgung B. ∠MAB : ∠AMB = 2 : 3 dan ∠MCB : ∠BMC = 3 : 4. Tentukan besar masing-masing sudut yang belum diketahui!

<p>Jawaban: ∠AMB = 54°, ∠MAB = 36°, ∠BMC≈ 51,43°</p><p>dan ∠MCB ≈ 38,57°.</p><p>&nbsp;</p><p>&nbsp;</p><p>Ingat konsep berikut:</p><p>Garis singgung lingkaran akan tegak lurus dengan jari-jari lingkaran yang melalui titik singgungnya dan membentuk sudut 90°.</p><p>Jumlah sudut dalam suatu segitiga adalah 180°.</p><p>&nbsp;</p><p>Diketahui AC adalah garis singgung lingkaran M dengan titik singgung B.</p><p>∠MAB : ∠AMB = 2 : 3&nbsp;</p><p>Maka ∠MAB = 2/3 ∠AMB</p><p>&nbsp;</p><p>dan ∠MCB : ∠BMC = 3 : 4.</p><p>Maka ∠MCB = 3/4 ∠BMC</p><p>&nbsp;</p><p>Karena AC adalah garis singgung lingkaran, maka ∠ABM = ∠MBC = 90°.</p><p>Perhatikan segitiga ABM, maka:</p><p>&nbsp; &nbsp;∠MAB + ∠AMB +∠ABM = 180°</p><p>2/3 ∠AMB + ∠AMB + 90° = 180°</p><p>&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;2/3 ∠AMB + ∠AMB = 90°</p><p>&nbsp; &nbsp;2/3 ∠AMB + 3/3 ∠AMB = 90°</p><p>&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; 5/3 ∠AMB = 90°</p><p>&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; ∠AMB = 90° : (5/3)</p><p>&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; ∠AMB = 90° x (3/5)</p><p>&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; ∠AMB = 54°</p><p>Sehingga ∠MAB = 2/3 x 54° = 36°.</p><p>&nbsp;</p><p>Perhatikan segitiga BCM, maka:</p><p>&nbsp; ∠MCB + ∠BMC + ∠MBC = 180°</p><p>&nbsp;3/4 ∠BMC + ∠BMC + 90° = 180°</p><p>&nbsp; &nbsp; 3/4 ∠BMC + 4/4 ∠BMC = 90°</p><p>&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;7/4 ∠BMC = 90°</p><p>&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; ∠BMC = 90° : (7/4)</p><p>&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; ∠BMC = 90° x (4/7)</p><p>&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; ∠BMC = (360/7)°</p><p>&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;∠BMC≈ 51,43°</p><p>Sehingga</p><p>∠MCB = 3/4 x (360/7)°</p><p>∠MCB = (270/7)°</p><p>∠MCB ≈ 38,57°</p><p>&nbsp;</p><p>Jadi, besar sudut ∠AMB = 54°, ∠MAB = 36°, ∠BMC≈ 51,43°</p><p>dan ∠MCB ≈ 38,57°.</p>