Tari H
14 Januari 2023 17:22
Iklan
Tari H
14 Januari 2023 17:22
Pertanyaan
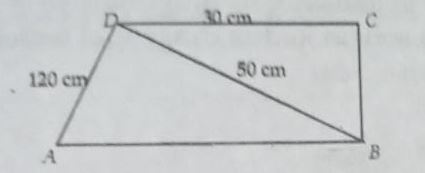
Perhatikan gambar berikut! Berapakah luas bangun ABCD?
1
1
Iklan
Y. Frando
01 Februari 2023 18:49
<p>Jawaban yang benar adalah (1.600√2 + 1.200) cm<sup>2</sup>.</p><p> </p><p>Pembahasan:</p><p>Ingat bahwa luas segitiga dirumuskan oleh:</p><p>L = ½ x alas x tinggi.</p><p> </p><p>Pada sebuah segitiga siku-siku berlaku juga teorema Pythagoras yaitu:</p><p>c<sup>2</sup> = a<sup>2</sup> + b<sup>2</sup>.</p><p> </p><p>Keterangan:</p><p>a = sisi mendatar segitiga (cm)</p><p>b = sisi tegak segitiga (cm)</p><p>c = sisi miring segitiga (cm).</p><p> </p><p>Dari gambar pada soal, luas bangun ABCD terdiri dari luas bangun BCD dan ABD yang keduanya adalah segitiga. Misalkan tinggi segitiga ABD adalah garis DE yang tegak lurus pada garis AB dan nilainya sama dengan panjang BC.</p><p>Cari nilai BC dari teorema Pythagoras, maka:</p><p>c<sup>2</sup> = a<sup>2</sup> + b<sup>2</sup></p><p>BD<sup>2</sup> = BC<sup>2</sup> + CD<sup>2</sup></p><p>50<sup>2</sup> = BC<sup>2</sup> + 30<sup>2</sup></p><p>2.500 - 900 = BC<sup>2</sup></p><p>BC = √1.600</p><p>BC = 40 cm.</p><p> </p><p>Sehingga:</p><p>BC = DE = 40 cm.</p><p> </p><p>Selanjutnya gunakan teorema Pythagoras untuk menghitung panjang garis AE.</p><p>c<sup>2</sup> = a<sup>2</sup> + b<sup>2</sup></p><p>AD<sup>2</sup> = AE<sup>2</sup> + DE<sup>2</sup></p><p>120<sup>2</sup> = AE<sup>2</sup> + 40<sup>2</sup></p><p>14.400 - 1.600 = AE<sup>2</sup></p><p>AE = √12.800</p><p>AE = 80√2 cm.</p><p> </p><p>Sehingga panjang AB adalah:</p><p>AB = AE + EB</p><p>AB = (80√2 + 30) cm.</p><p> </p><p>Maka, hitung luas masing-masing segitiga.</p><p>(i). Segitiga BCD</p><p>L<sub>BCD</sub> = 1/2 x CD x BC</p><p>L<sub>BCD</sub> = 1/2 x 30 x 40</p><p>L<sub>BCD</sub> = 600 cm<sup>2</sup>.</p><p> </p><p>(ii). Segitiga ABD</p><p>L<sub>ABD</sub> = 1/2 x AB x DE</p><p>L<sub>ABD</sub> = 1/2 x (80√2 + 30) x 40</p><p>L<sub>ABD</sub> = (1.600√2 + 600) cm<sup>2</sup>.</p><p> </p><p>Maka, luas ABCD adalah:</p><p>L<sub>ABCD</sub> = L<sub>BCD</sub> + L<sub>ABD</sub></p><p>L<sub>ABCD</sub> = 600 + (1.600√2 + 600)</p><p>L<sub>ABCD</sub> = (1.600√2 + 1.200) cm<sup>2</sup>.</p><p> </p><p>Jadi, luas bangun ABCD adalah (1.600√2 + 1.200) cm<sup>2</sup>.</p>
Jawaban yang benar adalah (1.600√2 + 1.200) cm2.
Pembahasan:
Ingat bahwa luas segitiga dirumuskan oleh:
L = ½ x alas x tinggi.
Pada sebuah segitiga siku-siku berlaku juga teorema Pythagoras yaitu:
c2 = a2 + b2.
Keterangan:
a = sisi mendatar segitiga (cm)
b = sisi tegak segitiga (cm)
c = sisi miring segitiga (cm).
Dari gambar pada soal, luas bangun ABCD terdiri dari luas bangun BCD dan ABD yang keduanya adalah segitiga. Misalkan tinggi segitiga ABD adalah garis DE yang tegak lurus pada garis AB dan nilainya sama dengan panjang BC.
Cari nilai BC dari teorema Pythagoras, maka:
c2 = a2 + b2
BD2 = BC2 + CD2
502 = BC2 + 302
2.500 - 900 = BC2
BC = √1.600
BC = 40 cm.
Sehingga:
BC = DE = 40 cm.
Selanjutnya gunakan teorema Pythagoras untuk menghitung panjang garis AE.
c2 = a2 + b2
AD2 = AE2 + DE2
1202 = AE2 + 402
14.400 - 1.600 = AE2
AE = √12.800
AE = 80√2 cm.
Sehingga panjang AB adalah:
AB = AE + EB
AB = (80√2 + 30) cm.
Maka, hitung luas masing-masing segitiga.
(i). Segitiga BCD
LBCD = 1/2 x CD x BC
LBCD = 1/2 x 30 x 40
LBCD = 600 cm2.
(ii). Segitiga ABD
LABD = 1/2 x AB x DE
LABD = 1/2 x (80√2 + 30) x 40
LABD = (1.600√2 + 600) cm2.
Maka, luas ABCD adalah:
LABCD = LBCD + LABD
LABCD = 600 + (1.600√2 + 600)
LABCD = (1.600√2 + 1.200) cm2.
Jadi, luas bangun ABCD adalah (1.600√2 + 1.200) cm2.
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke Forum
Biar Robosquad lain yang jawab soal kamu

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



