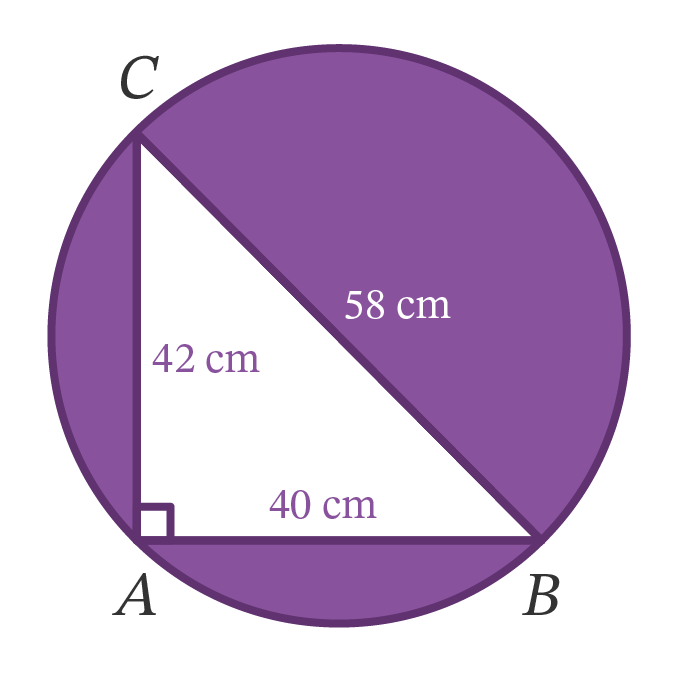
Panjang sisi-sisi sebuah segitiga adalah 40 cm, 58 crn, dan 42cm. Hitunglah: luas daerah yang berada di antara segitiga dan lingkaran luar segitiga.

<p>Jawaban : &nbsp; 1.800,74 cm²</p><p>&nbsp;</p><p>Ingat!</p><p>&gt;&gt; Jika a, b, dan c adalah sisi-sisi pada segitiga dengan c adalah sisi terpanjang dan memenuhi persamaan a² + b² = c² maka segitiga tersebut adalah segitiga siku-siku.</p><p>&nbsp;</p><p>&gt;&gt; Luas segitiga = (1/2). alas. tinggi</p><p>&nbsp;</p><p>&gt;&gt; Rumus jari-jari lingkaran luar segitiga</p><p>R = a.b.c/4L</p><p>Dimana</p><p>R : jari-jari lingkaran luar segitiga</p><p>L : luas segitiga</p><p>a,b,c : sisi-sisi pada segitiga</p><p>&nbsp;</p><p>&gt;&gt;Rumus luas lingkaran</p><p>L = πr²</p><p>Dimana</p><p>L : luas lingkaran</p><p>π = 22/7 atau 3,14</p><p>r : jari-jari lingkaran</p><p>&nbsp;</p><p>Diketahui</p><p>a = 42 cm</p><p>b = 40 cm</p><p>c = 58 cm</p><p>&nbsp;</p><p>Perhatikan perhitungan berikut</p><p>&nbsp;a² + b² = c²</p><p>42² + 40² &nbsp;= 58²</p><p>1.764 + 1.600 = 3.364</p><p>3.364 = 3.364</p><p>&nbsp;</p><p>Sehingga segitiga tersebut adalah segitiga siku-siku dengan sisi tegaknya adalah a dan b.</p><p>&nbsp;</p><p>Maka&nbsp;</p><p>Luas segitiga = (1/2) . a. b</p><p>Ls = (1/2) . 42 . 40</p><p>Ls = 840 cm²</p><p>&nbsp;</p><p>Jari-jari lingkaran luar</p><p>R = (abc)/(4Ls)&nbsp;</p><p>R = (42 . 40 . 58)/(4 . 840)&nbsp;</p><p>R = (42 . 40 . 58)/(40 . 84)</p><p>R = (42 . 58)/(84)</p><p>R = (42/84) . 58</p><p>R = 1/2 . 58</p><p>R = 29 cm</p><p>&nbsp;</p><p>Luas lingkaran luar</p><p>Lo = &nbsp;πr²</p><p>Lo = (3,14) . 29²</p><p>Lo = 3,14 . 841</p><p>Lo = 2.640,74 cm²</p><p>&nbsp;</p><p>Luas daerah didalam lingkaran tetapi diluar segitiga</p><p>= Lo - Ls</p><p>= 2.640,74 - 840</p><p>= 1.800,74 cm²</p><p>&nbsp;</p><p>Dengan demikian luas daerah didalam lingkaran tetapi diluar segitiga adalah &nbsp;1.800,74 cm².</p>