Moeh N
27 Januari 2023 03:21
Iklan
Moeh N
27 Januari 2023 03:21
Pertanyaan
Panjang sisi-sisi sebuah segitiga adalah 20 crn, 42 cm, dan 34 cm. Hitunglah: jarak titik pusat lingkaran dalam dengan titik sudut segitiga.
8
2
Iklan
E. Nur
Mahasiswa/Alumni Institut Teknologi Sepuluh Nopember
10 Juli 2023 03:32
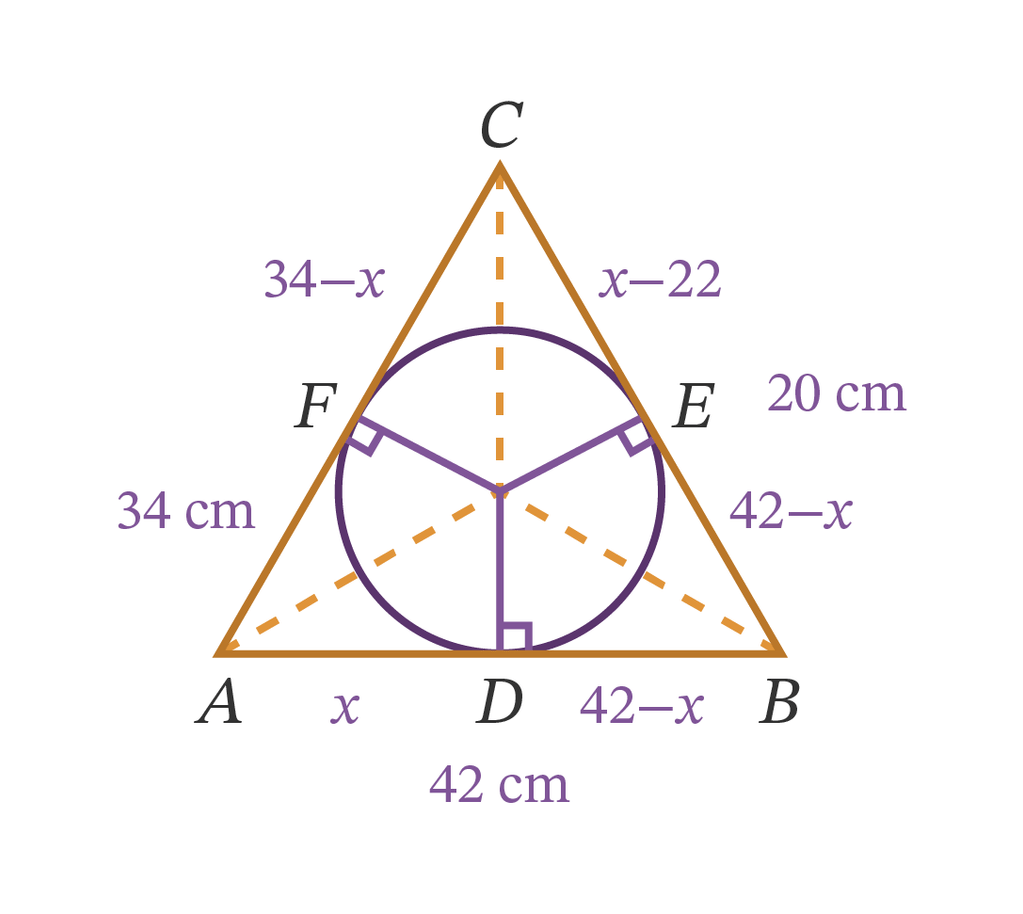
<p>Jawaban : 7√(13) cm, 7√(5) cm dan √(85) cm.</p><p> </p><p>Ingat</p><p>Panjang jari-jari lingkaran dalam segitiga dengan panjang sisi a,b, dan c adalah</p><p>r = L/s</p><p>L = √(s(s-a)(s-b)(s-c))</p><p>Dimana</p><p>r : jari-jari lingkaran dalam</p><p>s = (a+b+c)/2</p><p>L = luas segitiga</p><p> </p><p>>> Luas lingkaran = πr²</p><p> </p><p>>> Jika a, b, dan c adalah sisi-sisi pada segitiga siku-siku dimana c adalah sisi terpanjangnya maka berlaku</p><p>c = √(a² + b²)</p><p> </p><p>Diketahui</p><p>a = 20 cm</p><p>b = 42 cm</p><p>c = 34 cm</p><p> </p><p>Maka</p><p>s = (a+b+c)/2 = (20+42+34)/2 = 96/2 = 48</p><p>L = √(s(s-a)(s-b)(s-c))</p><p>L = √(48 (48-20)(48-42)(48-34))</p><p>L = √(48 . 28 . 6 . 14)</p><p>L = √(112.896)</p><p>L = 336 cm²</p><p> </p><p>Sehingga</p><p>r = L/s = 336/48 = 7 cm</p><p> </p><p>Perhatikan gambar terlampir, misalkan segitiga tersebut adalah segitiga ABC dan pusat lingkaran dalamnya adalah titik O, dan panjang AD = x maka</p><p>DB = 42 - x</p><p>EB = DB = 42 - x</p><p>CE = 20 - (42 - x) = 20 - 4 2 + x = x - 22</p><p>AF = AD = x</p><p>FC = 34 - x</p><p> </p><p>Sehingga</p><p>FC = CE</p><p>34 - x = x - 22</p><p>-x-x = -22 - 34</p><p>-2x = - 56</p><p>x = (-56)/(-2)</p><p>x = 28 cm</p><p> </p><p>AD = x = 28 cm</p><p>DB = 42 - x = 42 - 28 = 14 cm</p><p>CE = x -22 = 28 - 22 = 6 cm</p><p> </p><p>Maka</p><p>OA = √(AD² + r²)</p><p>OA = √(28² + 7²)</p><p>OA = √(784+49)</p><p>OA = √(833)</p><p>OA = 7√(13) cm</p><p> </p><p>OB = √(DB² + r²)</p><p>OB = √(14² + 7²)</p><p>OB = √(196+ 49)</p><p>OB = √(245) </p><p>OB = 7√(5) cm</p><p> </p><p>OC = √(CE² + r²)</p><p>OC = √(6² + 7²)</p><p>OC = √(36+49)</p><p>OC = √(85) cm</p><p> </p><p>Dengan demikian jarak titik sudut segitiga dengan titik pusat lingkaran dalam adalah 7√(13) cm, 7√(5) cm dan √(85) cm.</p>
Jawaban : 7√(13) cm, 7√(5) cm dan √(85) cm.
Ingat
Panjang jari-jari lingkaran dalam segitiga dengan panjang sisi a,b, dan c adalah
r = L/s
L = √(s(s-a)(s-b)(s-c))
Dimana
r : jari-jari lingkaran dalam
s = (a+b+c)/2
L = luas segitiga
>> Luas lingkaran = πr²
>> Jika a, b, dan c adalah sisi-sisi pada segitiga siku-siku dimana c adalah sisi terpanjangnya maka berlaku
c = √(a² + b²)
Diketahui
a = 20 cm
b = 42 cm
c = 34 cm
Maka
s = (a+b+c)/2 = (20+42+34)/2 = 96/2 = 48
L = √(s(s-a)(s-b)(s-c))
L = √(48 (48-20)(48-42)(48-34))
L = √(48 . 28 . 6 . 14)
L = √(112.896)
L = 336 cm²
Sehingga
r = L/s = 336/48 = 7 cm
Perhatikan gambar terlampir, misalkan segitiga tersebut adalah segitiga ABC dan pusat lingkaran dalamnya adalah titik O, dan panjang AD = x maka
DB = 42 - x
EB = DB = 42 - x
CE = 20 - (42 - x) = 20 - 4 2 + x = x - 22
AF = AD = x
FC = 34 - x
Sehingga
FC = CE
34 - x = x - 22
-x-x = -22 - 34
-2x = - 56
x = (-56)/(-2)
x = 28 cm
AD = x = 28 cm
DB = 42 - x = 42 - 28 = 14 cm
CE = x -22 = 28 - 22 = 6 cm
Maka
OA = √(AD² + r²)
OA = √(28² + 7²)
OA = √(784+49)
OA = √(833)
OA = 7√(13) cm
OB = √(DB² + r²)
OB = √(14² + 7²)
OB = √(196+ 49)
OB = √(245)
OB = 7√(5) cm
OC = √(CE² + r²)
OC = √(6² + 7²)
OC = √(36+49)
OC = √(85) cm
Dengan demikian jarak titik sudut segitiga dengan titik pusat lingkaran dalam adalah 7√(13) cm, 7√(5) cm dan √(85) cm.
· 3.8 (4)
Cella C
29 September 2024 14:43
Knp bisa dpt 7 akar 13?
Iklan
Ziyaul H
19 Mei 2024 09:44
panjang sisi sisi sebuah segitiga adalah 20cm,42cm,34cm hitunglah panjang jari lingkaran dalam segitiga
· 0.0 (0)
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



