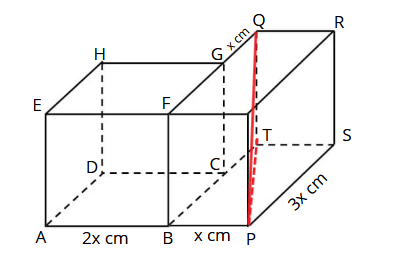
pada kubus ABCD. EFGH jika AP adalah perpanjangan rusuk AB:BP = 2:1 dan FQ adalah perpanjangan FG sehingga FP:FG = 3:2 maka tentukanlah jarak dari titik P dan Q

<p>Jawaban: x√14 cm</p><p>&nbsp;</p><p>Teorema Pythagoras:</p><p>c² = a² + b²</p><p>dengan:</p><p>c : panjang sisi miring segitiga siku-siku</p><p>a &amp; b : panjang sisi tegak segitiga siku-siku</p><p>&nbsp;</p><p>Misalkan panjang kubus adalah 2x cm, maka:</p><p>AB = FG = 2x cm</p><p>&nbsp;</p><p>AB/BP = 2/1</p><p>AB · 1/2 = BP</p><p>2x · 1/2 = BP</p><p>x = BP</p><p>BP = &nbsp;x cm</p><p>&nbsp;</p><p>Asumsikan FQ : FG = 3 : 2, maka:</p><p>FQ/FG = 3/2</p><p>FQ = 3/2 · FG</p><p>FQ = 3/2 · 2x</p><p>FQ = 3x cm</p><p>&nbsp;</p><p>FQ = FG + GQ</p><p>GQ = FQ - FG</p><p>GQ = 3x - 2x</p><p>GQ = x cm</p><p>&nbsp;</p><p>Maka,</p><p>TS = BP = x cm</p><p>PS = BT = 3x cm</p><p>QT = FB = 2x cm</p><p>&nbsp;</p><p>Perhatikan gambar!</p><p>Jarak titik P dan Q adalah PQ.</p><p>Dengan menggunakan Pythagoras, maka:</p><p>PT = √(PS² + TS²)</p><p>PT = √((3x)² + x²)</p><p>PT = √(9x² + x²)</p><p>PT = √(10x²) cm</p><p>&nbsp;</p><p>PQ = √(QT² + PT²)</p><p>PQ = √((2x)² + (√10x²)²)</p><p>PQ = √(4x² + 10x²)</p><p>PQ = √14x²&nbsp;</p><p>PQ = x√14 cm</p><p>&nbsp;</p><p>Jadi, jarak titik P dan Q adalah x√14 cm.</p>