Tetsu T
10 Januari 2023 07:12
Iklan
Tetsu T
10 Januari 2023 07:12
Pertanyaan
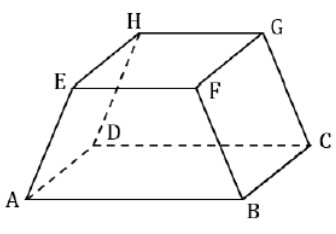
Pada gambar di bawah menunjukkan piramida terpotong ABCD.EFGH tegak beraturan dengan ABCD dan EFGH merupakan persegi yang saling sejajar dengan AB = 12 cm, EF = 8cm, dan AE = BF = CG = DH = 10cm. Hitung jarak antar titik. titik potong diagonal HF dan EG dengan titik potong AC dan BD.
1
1
Iklan
S. SheilaTeacherAssisstant
Mahasiswa/Alumni Universitas Pancasila
12 Januari 2023 00:23
<p><strong>Jawaban: 4√6 cm.</strong></p><p> </p><p><strong>Ingat!</strong></p><p><strong>Pada segitiga siku-siku berlaku Theorema Phytagoras:</strong></p><p><strong>c² = a² + b²</strong></p><p><strong>dimana</strong></p><p><strong>c = sisi miring</strong></p><p><strong>a dan b = sisi tegak/datar</strong></p><p> </p><p>Piramida terpotong ABCD.EFGH tegak beraturan.</p><p>ABCD dan EFGH persegi, maka </p><p>AB = BC = CD = DA = 12 cm</p><p>EF = FG = GH = HE = 8 cm</p><p>AE = BF = CG = DH = 10cm</p><p>Lihat gambar: </p><p>Titik potong HF dan EG adalah I.</p><p>Titik potong AC dan BD adalah J.</p><p>Maka, <strong>jarak titik potong diagonal HF dan EG dengan titik potong AC dan BD adalah IJ yang sejajar dengan tinggi trapesium ABFE yaitu EP dan FO.</strong></p><p>Sehingga, </p><p>AP = OB = ½(AB – EF)</p><p>= ½(12 – 8)</p><p>= ½(4)</p><p><strong>= 2 cm</strong></p><p> </p><p>BF² = BO² + OF²</p><p>10² = 2² + OF²</p><p>100 = 4 + OF²</p><p>OF² = 100 – 4</p><p>OF² = 96</p><p>OF = ±√96 (ambil yang positif karena jarak)</p><p><strong>OF = 4√6 cm</strong></p><p><strong>Sehingga IJ = FO = 4√6 cm.</strong></p><p> </p><p><strong><u>Dengan demikian, jarak titik potong diagonal HF dan EG dengan titik potong AC adalah 4√6 cm.</u></strong></p>
Jawaban: 4√6 cm.
Ingat!
Pada segitiga siku-siku berlaku Theorema Phytagoras:
c² = a² + b²
dimana
c = sisi miring
a dan b = sisi tegak/datar
Piramida terpotong ABCD.EFGH tegak beraturan.
ABCD dan EFGH persegi, maka
AB = BC = CD = DA = 12 cm
EF = FG = GH = HE = 8 cm
AE = BF = CG = DH = 10cm
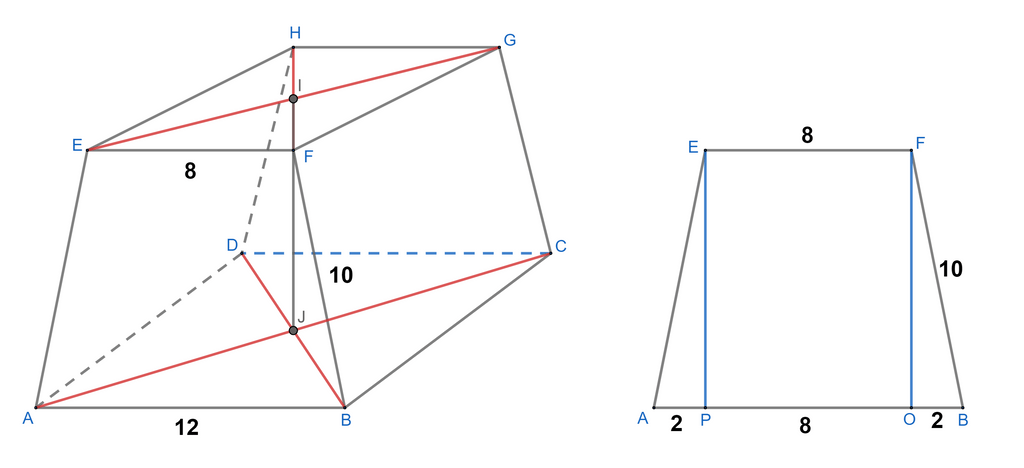
Lihat gambar:
Titik potong HF dan EG adalah I.
Titik potong AC dan BD adalah J.
Maka, jarak titik potong diagonal HF dan EG dengan titik potong AC dan BD adalah IJ yang sejajar dengan tinggi trapesium ABFE yaitu EP dan FO.
Sehingga,
AP = OB = ½(AB – EF)
= ½(12 – 8)
= ½(4)
= 2 cm
BF² = BO² + OF²
10² = 2² + OF²
100 = 4 + OF²
OF² = 100 – 4
OF² = 96
OF = ±√96 (ambil yang positif karena jarak)
OF = 4√6 cm
Sehingga IJ = FO = 4√6 cm.
Dengan demikian, jarak titik potong diagonal HF dan EG dengan titik potong AC adalah 4√6 cm.
· 2.0 (1)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



