Diketahui himpunan P = {-2, -1 , 0, 1, 2} dan Q = {0, 1, 2, 3, 4, 5}. Fungsi f adalah suatu fungsi dari himpunan P ke Q dengan aturan f{x) = x^2 + 1. b Tentukan domain, kodomain, dan range dari fungsi f

Question

Jawaban yang benar adalah {-2, -1 , 0, 1, 2}, {0, 1, 2, 3, 4, 5}, dan {1, 2, 5}.

Diketahui:

P = {-2, -1 , 0, 1, 2}

Q = {0, 1, 2, 3, 4, 5}

Fungsi f dari himpunan P ke Q dengan aturan f(x) = x^2 + 1

Ditanya:

Domain, kodomain, dan range dari fungsi f = ...?

Jawab:

Ingat konsep berikut!

(i) Domain adalah daerah asal.

(ii) Kodomain adalah daerah kawan.

(iii) Range adalah daerah hasil (anggota-anggota himpunan yang mempunyai kawan).

(iv) Diagram Kartesius menyatakan relasi antara dua himpunan dari pasangan berurutan yang kemudian dituliskan dalam bentuk dot (titik-titik) dalam sumbu mendatar dan sumbu tegak.

Dari soal di atas tentukan daerah hasil (range) dari himpunan P ke Q sesuai dengan fungsi f yang diberikan.

f(x) = x^2 + 1

f(-2) = (-2)^2 + 1 = 4 + 1 = 5.

f(-1) = (-1)^2 + 1 = 1 + 1 = 2.

f(0) = (0)^2 + 1 = 0 + 1 = 1.

f(1) = (1)^2 + 1 = 1 + 1 = 2.

f(2) = (2)^2 + 1 = 4 + 1 = 5.

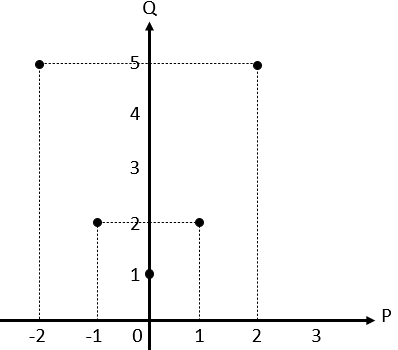
Dalam diagram Kartesius disajikan pada foto di bawah. Dari diagram Kartesius tersebut diperoleh hasil sebagai berikut:

(i) Domain: P = {-2, -1 , 0, 1, 2}.

(ii) Kodomain: Q = {0, 1, 2, 3, 4, 5}.

(iii) Range: R = {1, 2, 5}.

Jadi, domain, kodomain, dan range dari fungsi f berturut-turut adalah {-2, -1 , 0, 1, 2}, {0, 1, 2, 3, 4, 5}, dan {1, 2, 5}.

Diketahui himpunan P = {-2, -1 , 0, 1, 2} dan Q = {0, 1, 2, 3, 4, 5}. Fungsi f adalah suatu fungsi dari himpunan P ke Q dengan aturan f{x) = x^2 + 1. b Tentukan domain, kodomain, dan range dari fungsi f

Mau pemahaman lebih dalam untuk soal ini?

Pertanyaan serupa