Almira D
14 Januari 2023 00:51
Iklan
Almira D
14 Januari 2023 00:51
Pertanyaan
Diketahui f(x)=2x^(2)−4x+1. Tentukanlah : e. Grafik fungsinya
1
1
Iklan
C. Salsa
Mahasiswa/Alumni Universitas Gajah Mada
31 Januari 2023 14:26
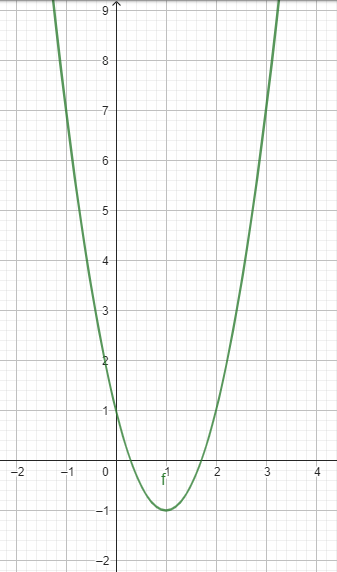
<p>Jawaban : grafik fungsi f(x)=2x^(2)−4x+1 adalah seperti pada gambar terlampir</p><p> </p><p>Konsep :</p><p>Untuk menggambar grafik fungsi kuadrat yaitu dengan mencari titik potong dengan sumbu x, sumbu y, serta dicari titik puncak/balik. </p><p>Jika diberikan persamaan y = ax^2 + bx + c, maka titik baliknya adalah (xp,yp) dengan </p><p>xp = -b/(2a) </p><p>yp = (b^2-4ac)/(-4a) </p><p> </p><p>Diketahui fungsi f(x)=2x^(2)−4x+1</p><p> </p><p>Kurva y = 2x^(2)−4x+1 memotong sumbu x ketika y=0 </p><p>y=0 </p><p>2x^(2)−4x+1 = 0 </p><p>x^(2)−2x+1/2 = 0 </p><p>(x-1)^(2)-1/2 = 0 </p><p>(x-1)^(2)-2/4 = 0 </p><p>(x-1)^(2) = 2/4</p><p>x-1 = ±√(2/4)</p><p>x-1 = ±(1/2)√(2)</p><p>x-1 = -(1/2)√(2) atau x-1 = (1/2)√(2)</p><p>x = 1-(1/2)√(2) atau x = 1+(1/2)√(2)</p><p>Titik potong sumbu X di (1-(1/2)√(2),0) dan (1+(1/2)√(2),0)</p><p> </p><p>Kurva y = 2x^(2)−4x+1 memotong sumbu y ketika x=0 </p><p>y = 2.0^2 -4.0+1</p><p>y = 0 -0+1</p><p>y = 1</p><p>Titik potong sumbu Y di (0,1)</p><p> </p><p>Lalu, cari titik baliknya. </p><p>Dari persamaan y = 2x^(2)−4x+1 diperoleh </p><p>a = 2 </p><p>b = -4</p><p>c = 1</p><p>sehingga </p><p>xp = -b/(2a)</p><p>xp = -(-4)/(2.2)</p><p>xp = 1</p><p>dan</p><p>yp = (b^2-4ac)/(-4a)</p><p>yp = ((-4)^2-4.2.1)/(-4.2)</p><p>yp = (16-8)/(-8)</p><p>yp = -1</p><p>Titik baliknya (1,-1)</p><p> </p><p>Untuk x = -1, maka</p><p>f(-1) = 2(-1)^(2)−4(-1)+1</p><p>= 2+4+1</p><p>= 7</p><p>Diperoleh (-1,7)</p><p> </p><p>Untuk x = 3, maka</p><p>f(3) = 2(3)^(2)−4(3)+1</p><p>= 18-12+1</p><p>= 7</p><p>Diperoleh (3,7)</p><p> </p><p>Lalu, gambarkan titik-titik tersebut.</p><p> </p><p>Jadi, grafik fungsi f(x)=2x^(2)−4x+1 adalah seperti pada gambar terlampir</p>
Jawaban : grafik fungsi f(x)=2x^(2)−4x+1 adalah seperti pada gambar terlampir
Konsep :
Untuk menggambar grafik fungsi kuadrat yaitu dengan mencari titik potong dengan sumbu x, sumbu y, serta dicari titik puncak/balik.
Jika diberikan persamaan y = ax^2 + bx + c, maka titik baliknya adalah (xp,yp) dengan
xp = -b/(2a)
yp = (b^2-4ac)/(-4a)
Diketahui fungsi f(x)=2x^(2)−4x+1
Kurva y = 2x^(2)−4x+1 memotong sumbu x ketika y=0
y=0
2x^(2)−4x+1 = 0
x^(2)−2x+1/2 = 0
(x-1)^(2)-1/2 = 0
(x-1)^(2)-2/4 = 0
(x-1)^(2) = 2/4
x-1 = ±√(2/4)
x-1 = ±(1/2)√(2)
x-1 = -(1/2)√(2) atau x-1 = (1/2)√(2)
x = 1-(1/2)√(2) atau x = 1+(1/2)√(2)
Titik potong sumbu X di (1-(1/2)√(2),0) dan (1+(1/2)√(2),0)
Kurva y = 2x^(2)−4x+1 memotong sumbu y ketika x=0
y = 2.0^2 -4.0+1
y = 0 -0+1
y = 1
Titik potong sumbu Y di (0,1)
Lalu, cari titik baliknya.
Dari persamaan y = 2x^(2)−4x+1 diperoleh
a = 2
b = -4
c = 1
sehingga
xp = -b/(2a)
xp = -(-4)/(2.2)
xp = 1
dan
yp = (b^2-4ac)/(-4a)
yp = ((-4)^2-4.2.1)/(-4.2)
yp = (16-8)/(-8)
yp = -1
Titik baliknya (1,-1)
Untuk x = -1, maka
f(-1) = 2(-1)^(2)−4(-1)+1
= 2+4+1
= 7
Diperoleh (-1,7)
Untuk x = 3, maka
f(3) = 2(3)^(2)−4(3)+1
= 18-12+1
= 7
Diperoleh (3,7)
Lalu, gambarkan titik-titik tersebut.
Jadi, grafik fungsi f(x)=2x^(2)−4x+1 adalah seperti pada gambar terlampir
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke Forum
Biar Robosquad lain yang jawab soal kamu

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



