Gracias M
13 Juni 2022 07:01
Iklan
Gracias M
13 Juni 2022 07:01
Pertanyaan
Buktikan T = 2π√(l/g) pada bandul yang digerakkan secara harmonic ! t ve pada bandul yang digerakkan secara harmonik !
20
1
Iklan
Y. Frando
25 September 2022 19:46
<p>Jawaban yang benar adalah terbukti bahwa periode bandul yang digerakkan secara harmonik yaitu T = 2π√(l/g).</p><p> </p><p>Pembahasan:</p><p>Konsep yang kita gunakan adalah periode getaran pada bandul. Ketika bandul diayunkan, maka terjadi gerak osilasi (gerak harmonis) pada bandul. Adapun periode osilasi ini dirumuskan oleh:</p><p> </p><p>T = 2π√(L/g).</p><p> </p><p>dengan:</p><p>T = periode getaran (s)</p><p>L = panjang tali (m)</p><p>g = percepatan gravitasi (m/s<sup>2</sup>).</p><p> </p><p>Persamaan di atas dapat dibuktikan sebagai berikut.</p><p>Dari gambar diagram gaya pada foto di bawah, terdapat gaya pemulih (Fp) yang bekerja pada bandul saat disimpangkan sejauh θ, yaitu:</p><p>Fp = -mg sin θ.</p><p> </p><p>Untuk sudut simpangan yang kecil, maka berlaku:</p><p>sin θ = tan θ = y/L.</p><p> </p><p>Sehingga dari hukum II Newton berlaku:</p><p>F = Fp</p><p>m x a = -mg sin θ</p><p>m x a = -mg (y/L).</p><p> </p><p>Percepatan gerak harmonik yang dihasilkan adalah:</p><p>a = - ω²y.</p><p> </p><p>Maka, dengan menggabungkan kedua persamaan di atas dapat diperoleh:</p><p>m x a = -mg (y/L)</p><p>m x (- ω²y) = -mg (y/L)</p><p>ω² = g/L</p><p>ω = √(g/L)</p><p>2π/T = √(g/L) ----> Ingat bahwa frekuensi sudut ω = 2π/T</p><p>T = 2π√(L/g).</p><p> </p><p>Jadi, terbukti bahwa pada bandul yang digerakkan secara harmonik berlaku T = 2π√(L/g).</p>
Jawaban yang benar adalah terbukti bahwa periode bandul yang digerakkan secara harmonik yaitu T = 2π√(l/g).
Pembahasan:
Konsep yang kita gunakan adalah periode getaran pada bandul. Ketika bandul diayunkan, maka terjadi gerak osilasi (gerak harmonis) pada bandul. Adapun periode osilasi ini dirumuskan oleh:
T = 2π√(L/g).
dengan:
T = periode getaran (s)
L = panjang tali (m)
g = percepatan gravitasi (m/s2).
Persamaan di atas dapat dibuktikan sebagai berikut.
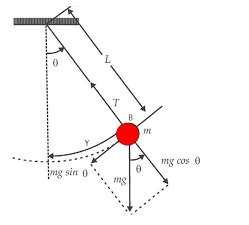
Dari gambar diagram gaya pada foto di bawah, terdapat gaya pemulih (Fp) yang bekerja pada bandul saat disimpangkan sejauh θ, yaitu:
Fp = -mg sin θ.
Untuk sudut simpangan yang kecil, maka berlaku:
sin θ = tan θ = y/L.
Sehingga dari hukum II Newton berlaku:
F = Fp
m x a = -mg sin θ
m x a = -mg (y/L).
Percepatan gerak harmonik yang dihasilkan adalah:
a = - ω²y.
Maka, dengan menggabungkan kedua persamaan di atas dapat diperoleh:
m x a = -mg (y/L)
m x (- ω²y) = -mg (y/L)
ω² = g/L
ω = √(g/L)
2π/T = √(g/L) ----> Ingat bahwa frekuensi sudut ω = 2π/T
T = 2π√(L/g).
Jadi, terbukti bahwa pada bandul yang digerakkan secara harmonik berlaku T = 2π√(L/g).
· 4.5 (8)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



