Tetsu T
10 Januari 2023 09:39
Iklan
Tetsu T
10 Januari 2023 09:39
Pertanyaan
Budi memiliki kamar tidur dengan panjang 5 m, lebar 5 m, dan tinggi 4 m. Di langit-langit kamar terdapat lampu yang letaknya tepat pada pusat bidang langit - langit. Pada salah dinding kamar dipasang saklar yang letaknya tepat di tengah - tengah dinding. Hitunglah jarak saklar ke lampu!
1
1
Iklan
S. SheilaTeacherAssisstant
Mahasiswa/Alumni Universitas Pancasila
11 Januari 2023 06:00
<p><strong>Jawaban: ½√41 m.</strong></p><p> </p><p><strong>Ingat!</strong></p><p><strong>Pada segitiga siku-siku berlaku Theorema Phytagoras:</strong></p><p><strong>c² = a² + b²</strong></p><p><strong>dimana</strong></p><p><strong>c = sisi miring</strong></p><p><strong>a dan b = sisi tegak/datar</strong></p><p> </p><p>Untuk soal di atas perhatikan gambar di bawah, kamar Budi berukuran p = 5 m, l = 5 m, dan t = 4 m.</p><p>Lampu di pusat langit-langit (A).</p><p>Saklar di tengah-tengah salah satu dinding yang berukuran l = 5 m dan t = 4 m, sehingga posisi saklar dimisalkan (B).</p><p><strong>Lihat segitiga ABC, jarak dari saklar ke lampu = AB = c, </strong></p><p><strong>dimana </strong></p><p><strong>AC = b = ½p = ½∙5 = 2,5 m</strong></p><p><strong>BC = a = ½t = ½∙4 = 2 m sehingga:</strong></p><p>c² = a² + b²</p><p>c² = 2² + 2,5²</p><p>c² = 4 + 6,25</p><p>c² = 10,25</p><p>c = ±√10,25</p><p>c = ±√(10¼)</p><p>c = ±√(41/4)</p><p><strong>c = ½√41 m (ambil yang positif karena jarak)</strong></p><p> </p><p><strong><u>Dengan demikian, jarak saklar ke lampu adalah ½√41 m.</u></strong></p>
Jawaban: ½√41 m.
Ingat!
Pada segitiga siku-siku berlaku Theorema Phytagoras:
c² = a² + b²
dimana
c = sisi miring
a dan b = sisi tegak/datar
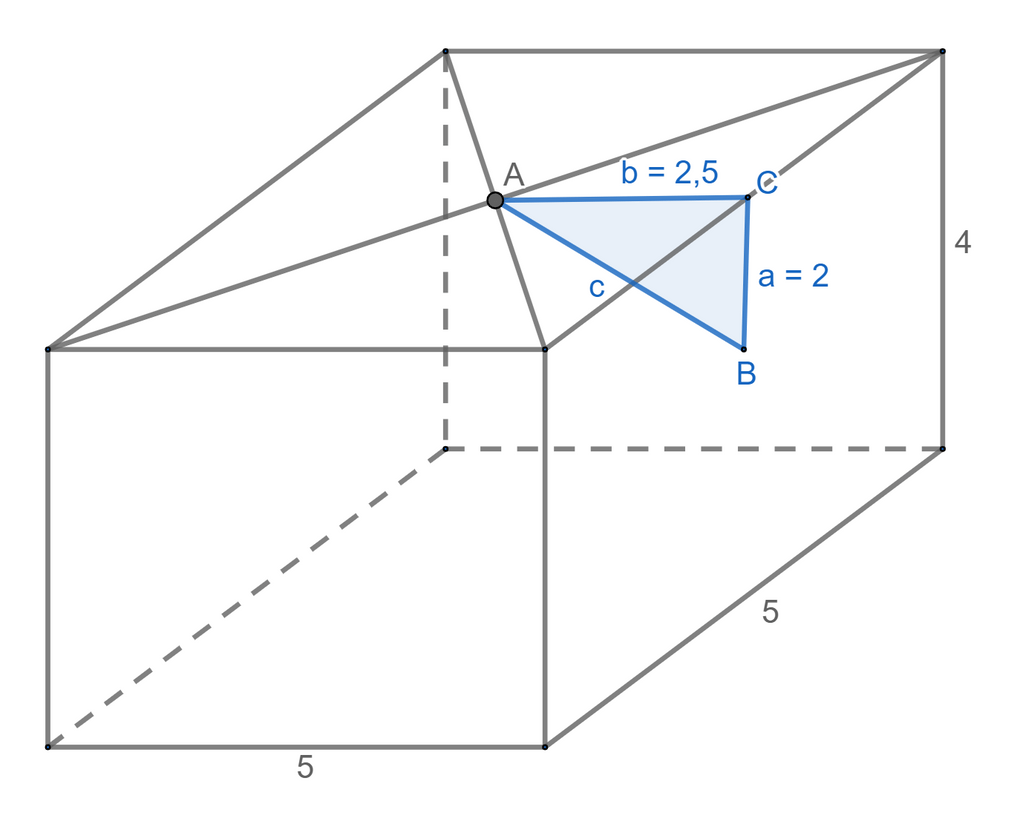
Untuk soal di atas perhatikan gambar di bawah, kamar Budi berukuran p = 5 m, l = 5 m, dan t = 4 m.
Lampu di pusat langit-langit (A).
Saklar di tengah-tengah salah satu dinding yang berukuran l = 5 m dan t = 4 m, sehingga posisi saklar dimisalkan (B).
Lihat segitiga ABC, jarak dari saklar ke lampu = AB = c,
dimana
AC = b = ½p = ½∙5 = 2,5 m
BC = a = ½t = ½∙4 = 2 m sehingga:
c² = a² + b²
c² = 2² + 2,5²
c² = 4 + 6,25
c² = 10,25
c = ±√10,25
c = ±√(10¼)
c = ±√(41/4)
c = ½√41 m (ambil yang positif karena jarak)
Dengan demikian, jarak saklar ke lampu adalah ½√41 m.
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



