Luna S
15 Januari 2023 00:03
Iklan
Luna S
15 Januari 2023 00:03
Pertanyaan
Buatlah sketsa grafik fungsi kuadrat dari y=2x^(2)-4x+2.
2
1
Iklan
D. Nuryani
Mahasiswa/Alumni Universitas Padjadjaran
08 Februari 2023 03:06
<p>Jawaban : terlampir</p><p> </p><p>Langkah menggambar fungsi kuadrat/parabola y = ax² + bx + c : <br>1. Menentukan titik potong sumbu X, y = 0<br>2. Menentukan titik potong sumbu Y, x = 0<br>3. Menentukan titik puncak (xp, yp) = (-b/2a, (b² - 4ac)/-4a)</p><p>4. Titik lain jika diperlukan dengan mengambil sembarang x kemudian substitusi ke y. <br>5. Hubungkan titik-titik yang telah didapat</p><p> </p><p>▪️ Rumus ABC mencari akar persamaan kuadrat ax² + bx + c = 0<br>x1,2 = (-b ± √(b²-4ac))/2a</p><p> </p><p>Diketahui</p><p>y=2x^(2)-4x+2</p><p>a = 2</p><p>b = -4</p><p>c = 2</p><p> </p><p>➡️ Titik potong sumbu X, y = 0</p><p>2x^(2)-4x+2 = 0</p><p>2(x-1)^(2) = 0</p><p>(x - 1)^(2) = 0</p><p>x = 1</p><p>(1, 0)</p><p> </p><p>➡️ Titik potong sumbu Y, x = 0</p><p>y = 2(0)^(2)-4(0)+2</p><p>y = 2</p><p>(0, 2)</p><p> </p><p>➡️ Titik puncak</p><p>(xp, yp) = (-b/2a, (b² - 4ac)/-4a)</p><p>= (4/2(2), ((-4)² - 4(2)(2))/-4(2))</p><p>= (4/4, (16-16)/-8)</p><p>= (1, 0)</p><p> </p><p>➡️ Titik lain</p><p>x = -1 ---> y=2(-1)^(2)-4(-1)+2</p><p>y = 2+4+2</p><p>y = 8</p><p>(-1, 8)</p><p> </p><p>x = 2 ---> y=2(2)^(2)-4(2)+2</p><p>y = 8 - 8 + 2</p><p>y = 2</p><p>(2, 2)</p><p> </p><p>x = 3 ---> y=2(3)^(2)-4(3)+2</p><p>y = 18 - 12 + 2</p><p>y = 8</p><p>(3, 8)</p><p> </p><p>Kemudian hubungan titik-titik tersebut sehingga berbentuk parabola sebagai berikut.</p>
Jawaban : terlampir
Langkah menggambar fungsi kuadrat/parabola y = ax² + bx + c :
1. Menentukan titik potong sumbu X, y = 0
2. Menentukan titik potong sumbu Y, x = 0
3. Menentukan titik puncak (xp, yp) = (-b/2a, (b² - 4ac)/-4a)
4. Titik lain jika diperlukan dengan mengambil sembarang x kemudian substitusi ke y.
5. Hubungkan titik-titik yang telah didapat
▪️ Rumus ABC mencari akar persamaan kuadrat ax² + bx + c = 0
x1,2 = (-b ± √(b²-4ac))/2a
Diketahui
y=2x^(2)-4x+2
a = 2
b = -4
c = 2
➡️ Titik potong sumbu X, y = 0
2x^(2)-4x+2 = 0
2(x-1)^(2) = 0
(x - 1)^(2) = 0
x = 1
(1, 0)
➡️ Titik potong sumbu Y, x = 0
y = 2(0)^(2)-4(0)+2
y = 2
(0, 2)
➡️ Titik puncak
(xp, yp) = (-b/2a, (b² - 4ac)/-4a)
= (4/2(2), ((-4)² - 4(2)(2))/-4(2))
= (4/4, (16-16)/-8)
= (1, 0)
➡️ Titik lain
x = -1 ---> y=2(-1)^(2)-4(-1)+2
y = 2+4+2
y = 8
(-1, 8)
x = 2 ---> y=2(2)^(2)-4(2)+2
y = 8 - 8 + 2
y = 2
(2, 2)
x = 3 ---> y=2(3)^(2)-4(3)+2
y = 18 - 12 + 2
y = 8
(3, 8)
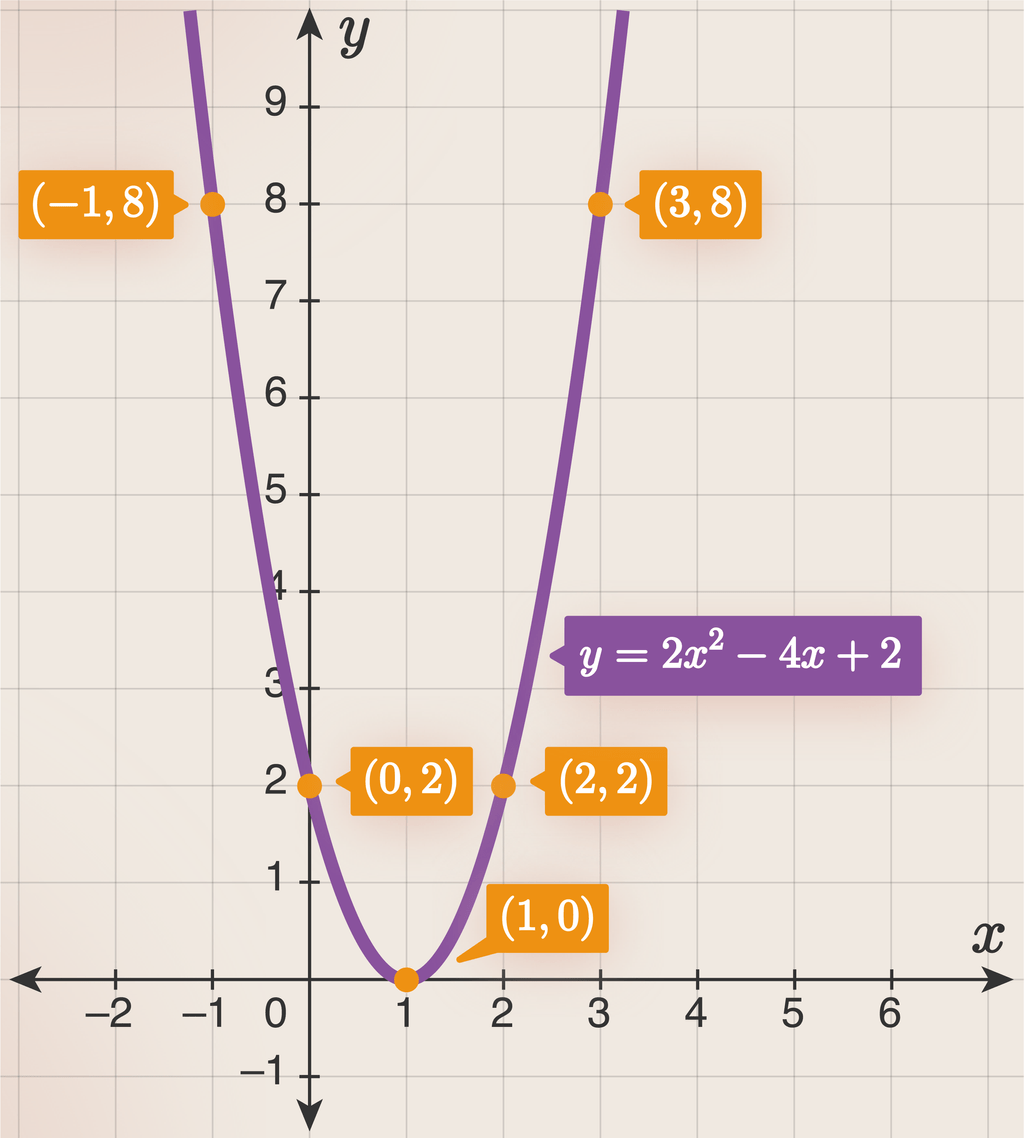
Kemudian hubungan titik-titik tersebut sehingga berbentuk parabola sebagai berikut.
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



