Fatima N
15 Januari 2023 08:50
Iklan
Fatima N
15 Januari 2023 08:50
Pertanyaan
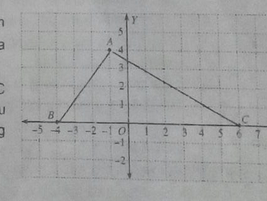
Berbentuk bangun apakah gabungan segitiga ABC dan bayangannya? Berikan alasanmu dengan menggunakan sifat-sifat yang berlaku pada bangun tersebut!
0
1
Iklan
C. Salsa
Mahasiswa/Alumni Universitas Gajah Mada
07 Februari 2023 23:20
<p>Jawaban : segitiga tumpul.</p><p> </p><p>Ingat! </p><p>Jika diberikan titik A(x1,y1) dan B(x2,y2) maka panjang AB adalah √((x1-x2)²+(y1-y2)²) </p><p>>>></p><p>Jika diberikan segitiga dengan panjang sisi a, b, c dengan c sisi terpanjang. </p><p>1. Jika c² > a²+b², maka segitiga tersebut merupakan segitiga tumpul </p><p>2. Jika c² = a²+b², maka segitiga tersebut merupakan segitiga siku-siku </p><p>3. Jika c² < a²+b², maka segitiga tersebut merupakan segitiga lancip </p><p>>>> Pencerminan terhadap sumbu X : </p><p>Jika titik (x,y) dicerminkan terhadap sumbu X, maka akan menghasilkan bayangan yaitu (x,-y)</p><p> </p><p>Diketahui segitiga ABC dengan koordinat A(-1,4), B(-4,0), dan C(6,0).</p><p> </p><p>Bayangan titik A(-1,4) jika dicerminkan terhadap sumbu X adalah</p><p>A'(-1,-4)</p><p> </p><p>Bayangan titik B(-4,0) jika dicerminkan terhadap sumbu X adalah</p><p>B'(-4,0)</p><p> </p><p>Bayangan titik C(6,0) jika dicerminkan terhadap sumbu X adalah</p><p>C'(6,0)</p><p> </p><p>Lalu, gambarkan segitiga ABC dan segitiga A'B'C'</p><p> </p><p>Diketahui segitiga ABC dengan koordinat A(-1,4), B(-4,0), dan C(6,0). </p><p> </p><p>AB = √((-1-(-4))²+(4-0)²) </p><p>AB = √(3²+4²) </p><p>AB = √(9+16) </p><p>AB = √25</p><p>AB = 5 satuan panjang </p><p> </p><p>AC = √((-1-6)²+(4-0)²) </p><p>AC = √((-7)²+4²) </p><p>AC = √(49+16) </p><p>AC = √65 satuan panjang </p><p> </p><p>BC = √((-4-6)²+(0-0)²) </p><p>BC = √((-10)²+0²) </p><p>BC = √(100+0) </p><p>BC = √100</p><p>BC = 10 satuan panjang </p><p> </p><p>Cek </p><p>BC² ... AB²+AC² </p><p>(10)² ... (5)²+(√65)² </p><p>100 ... 25+65</p><p>100 > 90 </p><p>Karena BC² > AB²+AC², maka segitiga ABC merupakan segitiga tumpul. </p><p> </p><p>Karena pencerminan tidak akan merubah bentuk dan panjang sisi, maka segitiga A'B'C' juga merupakan segitiga tumpul. </p><p> </p><p>Jadi, segitiga ABC dan segitiga A'B'C' merupakan segitiga tumpul.</p>
Jawaban : segitiga tumpul.
Ingat!
Jika diberikan titik A(x1,y1) dan B(x2,y2) maka panjang AB adalah √((x1-x2)²+(y1-y2)²)
>>>
Jika diberikan segitiga dengan panjang sisi a, b, c dengan c sisi terpanjang.
1. Jika c² > a²+b², maka segitiga tersebut merupakan segitiga tumpul
2. Jika c² = a²+b², maka segitiga tersebut merupakan segitiga siku-siku
3. Jika c² < a²+b², maka segitiga tersebut merupakan segitiga lancip
>>> Pencerminan terhadap sumbu X :
Jika titik (x,y) dicerminkan terhadap sumbu X, maka akan menghasilkan bayangan yaitu (x,-y)
Diketahui segitiga ABC dengan koordinat A(-1,4), B(-4,0), dan C(6,0).
Bayangan titik A(-1,4) jika dicerminkan terhadap sumbu X adalah
A'(-1,-4)
Bayangan titik B(-4,0) jika dicerminkan terhadap sumbu X adalah
B'(-4,0)
Bayangan titik C(6,0) jika dicerminkan terhadap sumbu X adalah
C'(6,0)
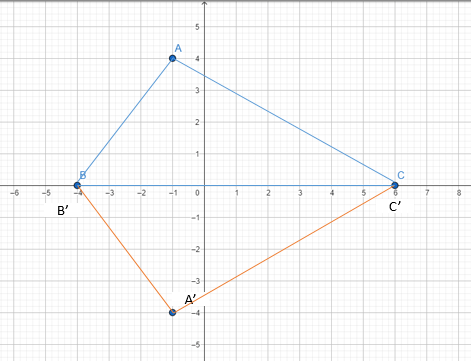
Lalu, gambarkan segitiga ABC dan segitiga A'B'C'
Diketahui segitiga ABC dengan koordinat A(-1,4), B(-4,0), dan C(6,0).
AB = √((-1-(-4))²+(4-0)²)
AB = √(3²+4²)
AB = √(9+16)
AB = √25
AB = 5 satuan panjang
AC = √((-1-6)²+(4-0)²)
AC = √((-7)²+4²)
AC = √(49+16)
AC = √65 satuan panjang
BC = √((-4-6)²+(0-0)²)
BC = √((-10)²+0²)
BC = √(100+0)
BC = √100
BC = 10 satuan panjang
Cek
BC² ... AB²+AC²
(10)² ... (5)²+(√65)²
100 ... 25+65
100 > 90
Karena BC² > AB²+AC², maka segitiga ABC merupakan segitiga tumpul.
Karena pencerminan tidak akan merubah bentuk dan panjang sisi, maka segitiga A'B'C' juga merupakan segitiga tumpul.
Jadi, segitiga ABC dan segitiga A'B'C' merupakan segitiga tumpul.
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke Forum
Biar Robosquad lain yang jawab soal kamu

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



