AP
Agustina P
25 November 2021 14:50
Iklan
AP
Agustina P
25 November 2021 14:50
Pertanyaan
2) Diketahui fungsi f (x)= -X²+12x-32 a.Tentukan titik potong dengan sumbu x b.Tentukan titik potong dengan sumbu y c.persamaan sumbu simetrinya d nilai maksimum/minimum e) Gambarlah grafik fungsi kuadratnya
4
3
Iklan
PA
P. Afrisno
Mahasiswa/Alumni Universitas Sebelas Maret
10 Januari 2022 05:09
Jawaban terverifikasi
Halo Agustina, terimakasih telah bertanya di roboguru. Kakak bantu jawab ya.
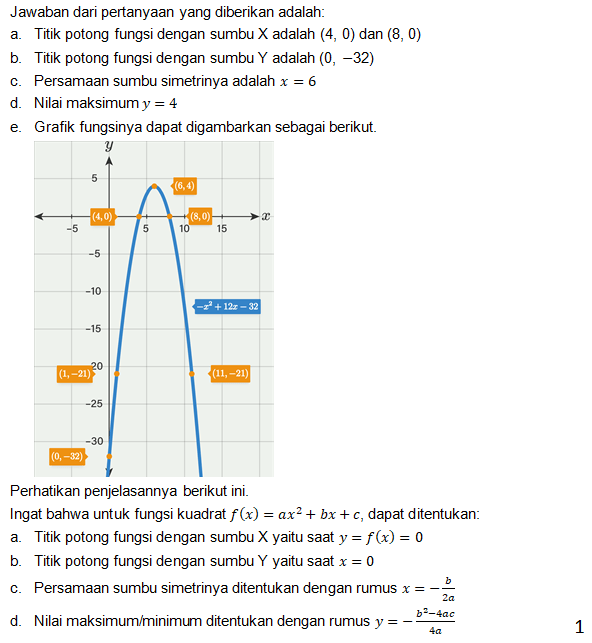


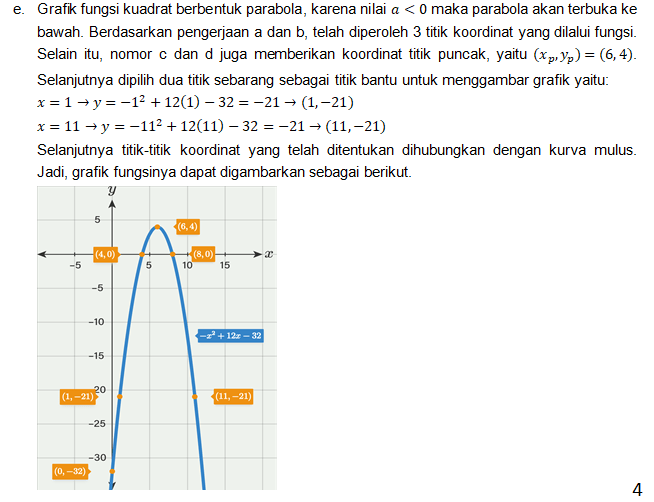
· 4.3 (7)
Iklan
MM
Masadepanjaemin M
25 November 2021 15:09
f(x) = -x²+12x-32 >> kalikan (-) f(x) = x²-12x+32 a= 1 b= -12 c= 32 a. titik potong dengan sumbu x >> y=0 x²-12x+32=0 (x-8) (x-4) 🔹x-8=0 🔹x=8 🔸x-4=0 🔸x=4 b. titik potong dengan sumbu y >> x=0 f(x) = x²-12x+32 f(0) = 0²-12(0) +32 f(0) = 32 c. Sumbu simetri x= -b/2a x= -(-12) /2*1 x= 12/2 x= 6 d. nilai maksimum y= -D/4a y= -(b²-4ac) /4a y= -((-12)²-4(1)(32)/4(1) y= -(144-128) /4 y= -16/4 y= -4
· 5.0 (1)
ST
S. Telaumbanua
26 November 2021 07:27
Jawaban yang benar adalah a. (8, 0) dan (4, 0) b. (0, 32) c. x = 6 d. 31 Hai Agustina P, terimakasih telah bertanya. Kakak bantu jawab ya Ingat! Bentuk umum fungsi kuadrat : y = f(x) = ax^2 + bx + c dengan a ≠ 0 a. f(x)= -x² + 12x - 32, memotong sumbu x jika y = 0 Maka di peroleh : -x² + 12x - 32 = 0 Sama-sama di kali (-1) x² - 12x + 32 = 0 (x - 8)(x - 4) = 0 x - 8 = 0 atau x - 4 = 0 x = 8 <--- ---> x = 4 Jadi titik potong pada sumbu x adalah (8, 0) dan (4, 0) b. f(x)= -x² + 12x - 32, memotong sumbu y jika x = 0 maka di peroleh : f(x)= x² - 12x + 32 f(0) = (0)^2 + 12(0) + 32 f(0) = 32 Jadi, titik potong pada sumbu y adalah (0, 32) c. Rumus sumbu simetri yaitu x = -b/2a f(x)= x² - 12x + 32 dengan a = 1, b = -12 dan c = 32 Maka diperoleh : x = -b/2a x = -(-12)/(2(1)) x = 12/2 x = 6 Jadi, sumbu simentrinya adalah 6 d. Rumus menentukan nilai maksimum/minimum yaitu Nilai ekstrim(max/min) = (b^2 - 4ac)/(-4a) Maka di peroleh : Nilai ekstrim(max/min) = (b^2 - 4ac)/(-4a) = ((-12)^2 - 4.1.32)/(-4.1) = (24 - 128)/(-4) = (-124)/(-4) = 31 Jadi, nilai maksimum/minimum adalah 31 Semoga dapat membantu
· 5.0 (1)
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



