Pertanyaan

Dua muatan q sebesar 2 , 0 × 1 0 − 6 C dipegang tetap sehingga berjarak d = 20 cm satu sama lain seperti gambar. Berapakah energi potensial total konfigurasi tersebut jika muatan q 3 telah berada di titik C ?

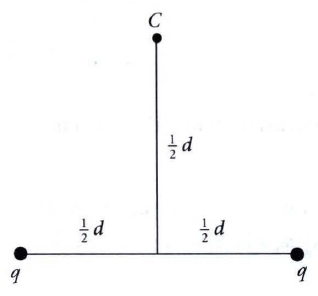
Dua muatan q sebesar $2, 0 \times 1 0^{- 6} C$ dipegang tetap sehingga berjarak d = 20 cm satu sama lain seperti gambar. Berapakah energi potensial total konfigurasi tersebut jika muatan $q_{3}$ telah berada di titik C?

N. Puspita

Master Teacher

Jawaban terverifikasi

Jawaban

energi potensial sistem dengan 3 muatan adalah 0,69 J (nilai mutlak).

Pembahasan

Diketahui: Ditanyakan: Energi potensial sistem dengan 3 muatan? Jawab: Energi potensial sistem dengan banyak muatan adalah gabungan seluruh energi potensial antara pasangan-pasangan muatan dalam sistem: Dengan demikian, energi potensial sistem dengan 3 muatan adalah 0,69 J (nilai mutlak).

Diketahui:

undefined

Ditanyakan:

Energi potensial sistem dengan 3 muatan?

Jawab:

Energi potensial sistem dengan banyak muatan adalah gabungan seluruh energi potensial antara pasangan-pasangan muatan dalam sistem:

$begin mathsize 14px style table attributes columnalign right center left columnspacing 0px end attributes row cell E p subscript t o t a l end subscript end cell equals cell k open parentheses fraction numerator q subscript 1 q subscript 2 over denominator r subscript 12 end fraction plus fraction numerator q subscript 1 q subscript 3 over denominator r subscript 13 end fraction plus fraction numerator q subscript 2 q subscript 3 over denominator r subscript 23 end fraction close parentheses end cell row blank equals cell k open parentheses q subscript 1 squared over r subscript 12 plus q subscript 1 squared over r subscript 13 plus q subscript 2 squared over r subscript 23 close parentheses end cell row blank equals cell open parentheses 9 times 10 to the power of 9 close parentheses open parentheses fraction numerator open parentheses 2 times 10 to the power of negative 6 end exponent close parentheses squared over denominator 2 times 10 to the power of negative 1 end exponent end fraction plus fraction numerator open parentheses 2 times 10 to the power of negative 6 end exponent close parentheses squared over denominator 2 times 10 to the power of negative 1 end exponent end fraction plus fraction numerator open parentheses 2 times 10 to the power of negative 6 end exponent close parentheses squared over denominator 2 times 10 to the power of negative 1 end exponent end fraction close parentheses end cell row blank equals cell open parentheses 9 close parentheses open parentheses 4 over 2 plus fraction numerator 4 over denominator square root of 2 end fraction plus fraction numerator 4 over denominator square root of 2 end fraction close parentheses open parentheses 10 to the power of 9 times 10 to the power of negative 12 end exponent over 10 to the power of negative 1 end exponent close parentheses end cell row cell E p subscript t o t a l end subscript end cell equals cell 9 open parentheses 2 plus fraction numerator 8 over denominator square root of 2 end fraction close parentheses times 10 to the power of negative 2 end exponent equals bold 0 bold comma bold 69 bold space bold J end cell end table end style$

Dengan demikian, energi potensial sistem dengan 3 muatan adalah 0,69 J (nilai mutlak).

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

5.0 (1 rating)

Pertanyaan serupa

Tiga buah partikel bermassa sama, m = 5 g dan mempunyai muatan yang sama, q = 3 , 0 × 1 0 − 8 C . Ketiganya terletak pada suatu garis lurus seperti tampak dalam gambar di samping. Berapakah besar ener...

0.0

Jawaban terverifikasi

Diketahui lima buah muatan listrik terletak seperti gambar berikut. Besar energi potensial listrik yang dialami muatan 5 mCadalah ....

5.0

Jawaban terverifikasi

Perhatikan gambar berikut! Muatan q 1 sebesar 8 µC diletakkan di pusat koordinat, sedangkan q 2 sebesar -3 µC diletakkan pada koordinat (3, 0). Jika muatan +4 µC diletakkan di titik P pada koord...

5.0

Jawaban terverifikasi

Jika kita memiliki muatan q 1 , q 2 dan q 3 dengan posisi diilustrasikan pada gambar di bawah, maka bagaimanakah alur yang kita kerjakan untuk mencari energi potensial listrik pada titik pengamatan P!

0.0

Jawaban terverifikasi

Beda potensial dua pelat sejajar adalah 200 volt. Sebuah proton bermassa 1 , 6 × 1 0 − 27 kg dan bermuatan 1 , 6 × 1 0 − 19 C yang beradadi pelat B bergerak menuju pelat A. Apabila di antara dua pelat...

4.9

Jawaban terverifikasi