Persamaan garis yang memotong sumbu X dan sumbu Y di titik (a, 0) dan (0, b) dapat ditentukan dengan rumus berikut.
ax+by=1
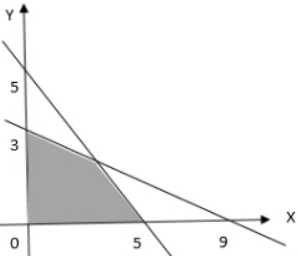
Sistem pertidaksamaan yang himpunan penyelesaiannya ditunjukkan oleh daerah yang diarsir di atas, dapat ditentukan dengan langkah berikut.
Perhatikan garis yang memotong sumbu X dan sumbu Y di titik (5, 0) dan (0, 5). Dapat ditentukan persamaan garis tersebut sebagai berikut.
5x+5yx+y==15
Karena garis yang terbentuk adalah garis penuh (bukan garis putus-putus) dan daerah yang diarsir berada di bawah/kiri garis maka diperoleh pertidaksamaan x+y≤5.
Selanjutnya, perhatikan garis yang memotong sumbu X dan sumbu Y di titik (9, 0) dan (0, 3). Dapat ditentukan persamaan garis tersebut sebagai berikut.
9x+3y3x+9y==127
Karena garis yang terbentuk adalah garis penuh (bukan garis putus-putus) dan daerah yang diarsir berada di bawah/kiri garis maka diperoleh pertidaksamaan 3x+9y≤27.
Karena daerah yang diarsir ada di atas sumbu X dan di kanan sumbu Y, maka diperoleh pertidaksamaan x≥0 dan y≥0.
Sehingga diperoleh sistem pertidaksamaan yang himpunan penyelesaiannya ditunjukkan oleh daerah yang diarsir di atas yaitu: x+y≤5; 3x+9y≤27; x≥0; y≥0.
Jadi, jawaban yang benar adalah A.