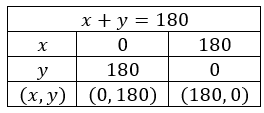Pertanyaan

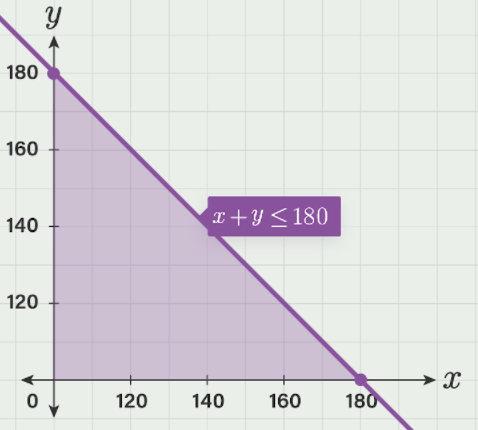
Bu Markamah seorang penjual buah di Pasar Mranggen. la membeli apel dengan harga Rp 15.000,00 per kg dan anggur seharga Rp 20.000,00 per kg. Bu Markamah dapat menjual apel dengan harga Rp 18.000,00 per kg dan anggur dengan harga Rp 25.000,00 per kg. Bu Markamah hanya dapat menjual kedua jenis buah itu sebanyak 180 kg saja setiap hari. a. Buatlah model matematika dari persoalan tersebut dengan memisalkan banyak apel x kg dan banyak anggur y kg! b. Gambarlah daerah penyelesaiannya!

Bu Markamah seorang penjual buah di Pasar Mranggen. la membeli apel dengan harga Rp 15.000,00 per kg dan anggur seharga Rp 20.000,00 per kg. Bu Markamah dapat menjual apel dengan harga Rp 18.000,00 per kg dan anggur dengan harga Rp 25.000,00 per kg. Bu Markamah hanya dapat menjual kedua jenis buah itu sebanyak 180 kg saja setiap hari.

a. Buatlah model matematika dari persoalan tersebut dengan memisalkan banyak apel $x$ kg dan banyak anggur $y$ kg!
b. Gambarlah daerah penyelesaiannya!

L. Rante

Master Teacher

Mahasiswa/Alumni Universitas Negeri Makassar

Jawaban terverifikasi

Pembahasan

a. Model matematika Bu Markamah hanya dapat menjual kedua jenis buah itu sebanyak saja setiap hari, maka dan menyatakan banyak sesuatu (selalu bernilai positif) maka Keuntungan dari penjualan apel/kg adalah Keuntungan dari penjualan anggur/kg adalah Maka total keuntungannya adalah Jadi model matematikanya yaitu Fungsi kendala Fungsi tujuan (maksimum) b. Gambardaerah penyelesaian Titik potong garis dengan sumbu koordinat Uji titik Grafik

a. Model matematika

x equals banyak space apel space open parentheses kg close parentheses y equals banyak space anggur space open parentheses kg close parentheses

Bu Markamah hanya dapat menjual kedua jenis buah itu sebanyak 180 space kg saja setiap hari, maka

x plus y less or equal than 180

dan menyatakan banyak sesuatu (selalu bernilai positif) maka

x greater or equal than 0 y greater or equal than 0

Keuntungan dari penjualan apel/kg adalah Rp 18.000 comma 00 minus Rp 15.000 comma 00 equals Rp 3.000 comma 00
Keuntungan dari penjualan anggur/kg adalah Rp 25.000 comma 00 minus Rp 20.000 comma 00 equals Rp 5.000 comma 00
Maka total keuntungannya adalah

f open parentheses x comma space y close parentheses equals 3.000 x plus 5.000 y

Jadi model matematikanya yaitu
Fungsi kendala

table attributes columnalign right center left columnspacing 0px end attributes row cell x plus y end cell less or equal than 180 row x greater or equal than 0 row y greater or equal than 0 end table

Fungsi tujuan

f open parentheses x comma space y close parentheses equals 3.000 x plus 5.000 y (maksimum)

b. Gambar daerah penyelesaian

Titik potong garis x plus y equals 180 dengan sumbu koordinat

Uji titik open parentheses 0 comma space 0 close parentheses

table attributes columnalign right center left columnspacing 0px end attributes row cell x plus y end cell less or equal than 180 row cell open parentheses 0 close parentheses plus open parentheses 0 close parentheses end cell less or equal than 180 row 0 less or equal than cell 180 space left parenthesis memenuhi right parenthesis end cell end table

x greater or equal than 0 space rightwards arrow daerah space sebelah space kanan space sumbu space y y greater or equal than 0 rightwards arrow daerah space bagian space atas space sumbu space x

Grafik

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

1.0 (1 rating)

Carisaa

Jawaban tidak sesuai

Pertanyaan serupa

Suatu perusahaan transportasi harus mendistribusikan 1.200 paket (yang besarnya sama) melalui dua truk pengangkut. Truk 1 memuat 200 paket untuk setiap pengangkutan dan truk 2 memuat 80 paket untuk se...

4.5

Jawaban terverifikasi

PT Usaha Rotanindo di Cirebonmemproduksi dua jenis mebel rotan, yaitujenis kursi dan meja. Kapasitas produksiperusahaan tidak kurang dari 1.000 unitbarang per bulan. Dari bagian marketing,diperoleh in...

5.0

Jawaban terverifikasi

Seorang pemborong mempunyaipersediaan 100 kaleng cat warna hijaudan 240 kaleng cat warna abu-abu.Pemborong tersebut mendapat order untuk mengecat ruang tamu dan ruang tidur disuatu gedung. Setelah dik...

3.0

Jawaban terverifikasi

Seorang pedagang ponsel memilikimodal sebesar Rp 49.600.000 , 00 untukmenjual dua jenis ponsel sebanyak-banyaknya 25 unit. Pedagang tersebutakan menjual ponsel jenis android danjenis biasa dengan harg...

4.7

Jawaban terverifikasi

Sebuah pesawat mempunyai tempat duduk 48 kursi. Penumpang kelas utama boleh membawa bagasi 60 kg, sedangkan kelas ekonomi 20 kg. Harga tiket kelas utama Rp 150.000 , 00 dan kelas ekonomi Rp 100.000 , ...

4.7

Jawaban terverifikasi