Dengan persediaan 2 kg gula dan 3 kg tepung akan dibuat dua jenis kue setiap kue a memerlukan 20 gram gula dan 40 gram tepung sedangkan kue B memerlukan 25 gram gula dan 30 gram tepung jika kue A dan B masing-masing dijual dengan keuntungan Rp.400,00/buah dan Rp350,00/buah maka banyak masing-masing kue yang dibuat agar keuntungan maksimum

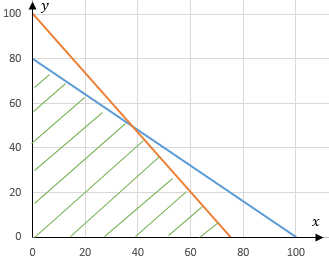
Halo Imelda. Jawaban : kue A yang dibuat sebanyak 37 kue dan kue B sebanyak 50 kue Langkah-langkah membuat model matematika pada program linear: 1. Buat pemisalan untuk unsur-unsur yang belum diketahui dalam bentuk variabel x dan y 2. Buat sistem pertidaksamaan linear dari hal-hal yang diketahui (fungsi kendala) Misalkan x : banyak kue A y : banyak kue B ------------------------------------------------- |.........|...Gula..|Tepung....|Keuntungan..| |_____|______|________|___________| |kue A|...20 g...|....40 g.....|.........400........| |_____|______|________|___________| |kue B|...25 g...|....30 g.....|.........350.......| |_____|______|________|___________| |..........|2.000 g|..3.000 g...|.....................| |_______________________________| Kendala Gula : 20x+25y≤2.000 -> bagi dengan 5 4x+5y≤400 Kendala Tepung : 40x+30y≤3.000 -> bagi dengan 10 4x+3y≤300 Model matematikanya adalah Maksimumkan 400 x + 350 y dengan kendala 4x+5y≤400 4x+3y≤300 x≥0, y≥0 Lalu, gambar daerah penyelesaiannya. Pertama, gambar garis 4x+5y=400. Substitusi x=0 4(0)+5y=400 5y=400 y=80 (0,80) Substitusi y=0 4x+5(0)=400 4x=400 x=100 (100,0) Uji titik: Pilih (0,0) 4(0)+5(0) ... 400 0 ≤ 400 Karena 4x+5y≤400 maka yang diarsir adalah daerah yang memuat titik (0,0). Kedua, gambar garis 4x+3y=300. Substitusi x=0 4(0)+3y=300 3y=300 y=100 (0,100) Substitusi y=0 4x+3(0)=300 4x=300 x=75 (75,0) Uji titik: Pilih (0,0) 4(0)+3(0) ... 300 0 ≤ 300 Karena 4x+3y≤300 maka yang diarsir adalah daerah yang memuat titik (0,0). Karena x≥0, y≥0 maka daerah yang diarsir adalah daerah di kuadran I. Gambar daerah penyelesaian seperti pada gambar terlampir. Titik sudut pada daerah yang diarsir adalah (0,0), (0,80), (75,0), dan titik potong kedua garis. Titik potong 4x+5y=400 4x+3y=300 __________- 2y=100 y=50 dan 4x+5(50)=400 4x+250=400 4x=150 x=150/4 x=75/2 (75/2,50) Cek pada fungsi tujuannya Untuk (0,0) diperoleh 400 (0) + 350 (0) = 0 Untuk (0,80) diperoleh 400 (0) + 350 (80) = 28.000 Untuk (75,0) diperoleh 400 (75) + 350 (0) = 30.000 Untuk (75/2,50) diperoleh 400 (75/2) + 350 (50) = 15.000 + 17.500 = 32.500 Keuntungan maksimum terjadi ketika membuat 75/2 = 37,5 (dibulatkan ke bawah) ≈ 37 kue A dan 50 kue B Jadi, kue A yang dibuat sebanyak 37 kue dan kue B sebanyak 50 kue